Предмет: Математика,
автор: vitekgorlov
Помогите, пожалуйста.
Заранее спасибо, с Новым Годом Вас и Рождеством!
Приложения:
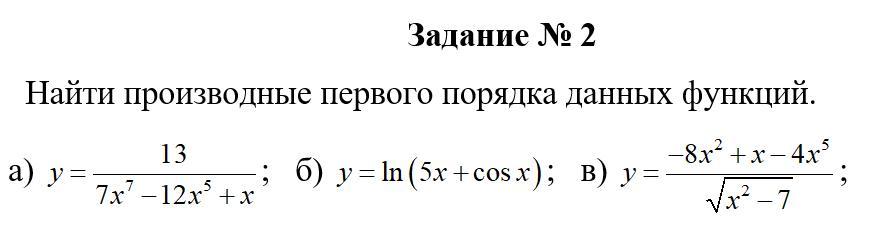
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
а)
б)
в)
Похожие вопросы
Предмет: Немецкий язык,
автор: solovyhtatjana
Предмет: Русский язык,
автор: kati198775
Предмет: Русский язык,
автор: Avt3Krishtom
Предмет: Математика,
автор: ghfaa
Предмет: Алгебра,
автор: 1239844