Помогите очень срочно
Нужно сделать исследование функции и построить график
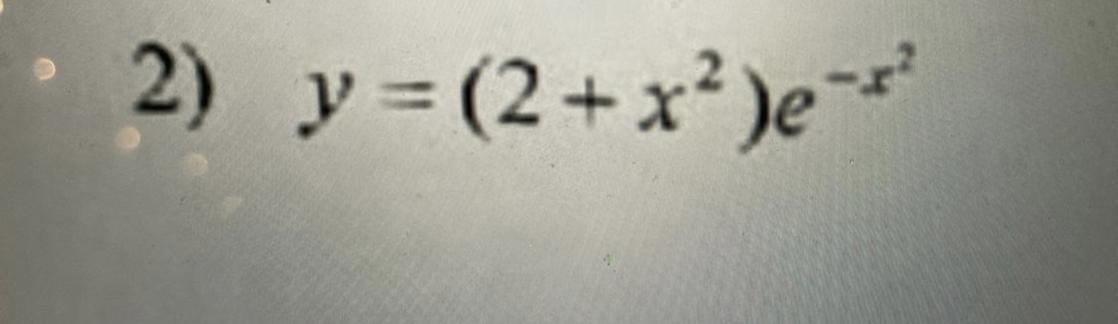
Ответы
Объяснение:
1. ОДЗ: х ∈ R
или х ∈ (-∞; +∞)
2. Четность, нечетность.
y(-x) = y(x) ⇒ четная
3. Пересечение с осями.
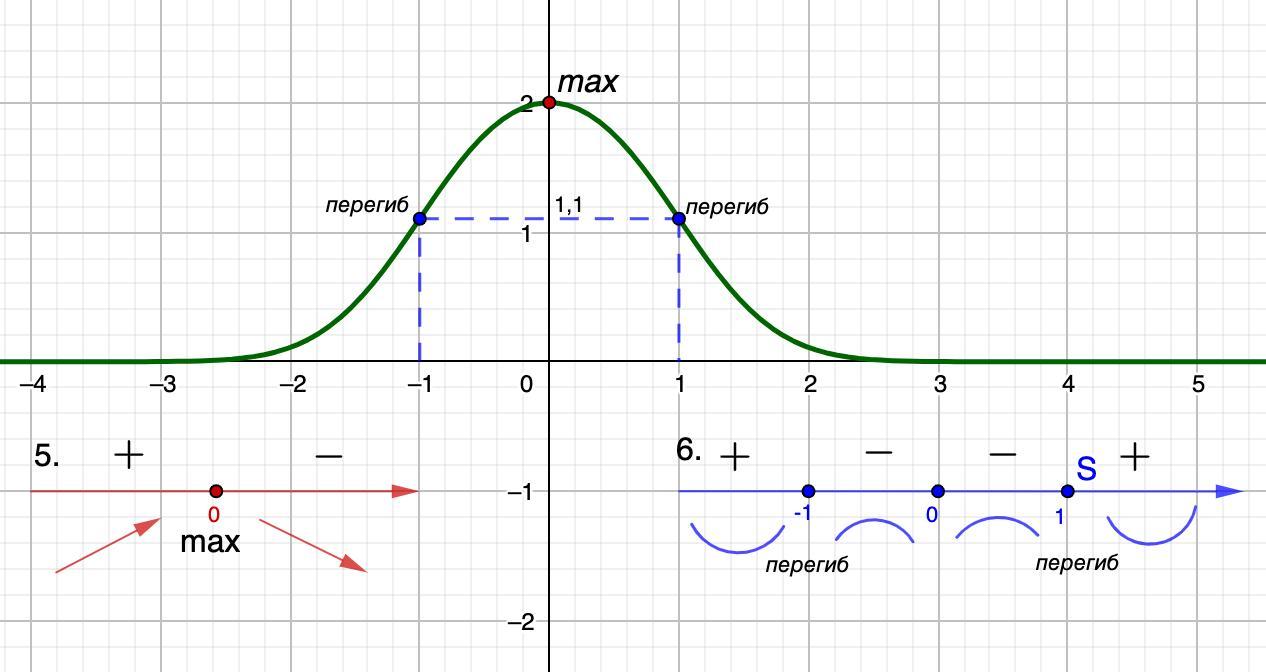
1) х = 0 ⇒ у = 2
2) у > 0 ⇒ ось 0х не пересекает.
4. Асимптоты.
1) Вертикальных асимптот нет.
2) Наклонная: y = kx + b
y = 0 - горизонтальная асимптота.
5. Возрастание, убывание, экстремумы.
Найдем производную:
Приравняем к 0 и найдем корни:
Найдем знаки производной на промежутках. Если "+" - возрастает, "-" - убывает.
Возрастает при х ∈ (-∞; 0]
Убывает при х ∈ [0; +∞)
См. рис.
6. Выпуклость, вогнутость.
Найдем производную второго порядка.
Приравняем к 0 и найдем корни:
Заменим переменную:
t > 0 ⇒ x² = 1
x₁ = 1; x₂=-1
Найдем знаки второй производной на промежутках.
( См. рисунок.)
x перегиба = ±1
При х ∈ (-∞; -1] ∪ [1; +∞) - вогнута;
при х ∈ [-1; 1] - выпукла.
Строим график.