Предмет: Геометрия, автор: Deimassah

Решите плиз две задачи С ПОШАГОВЫМИ РЕШЕНИЯМИ, сорян что задачи на мове. Кстати, с Новым 2022 Годом!!!
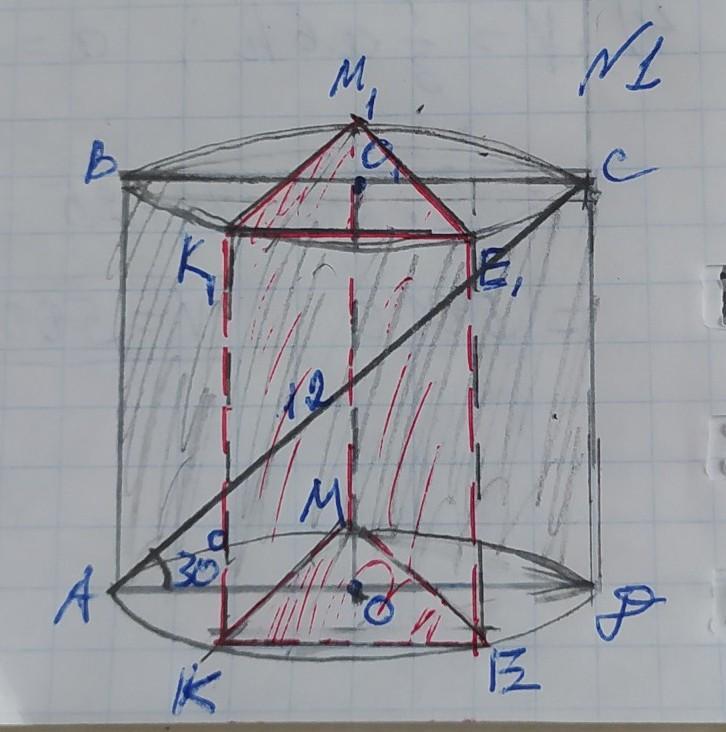
1. Діагональ осьового перерізу циліндра дорівнює 12 см і утворює з площиною основи кут 30 градусів. Знайдіть площу бічної поверхні правильної трикутної призми, вписаної в циліндр.
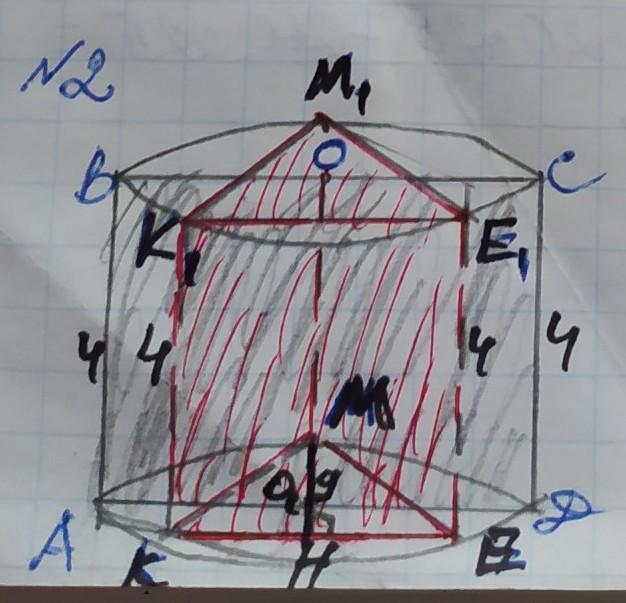
2. Висота основи правильної трикутної призми дорівнює 9 см, а бічне ребро призми - 4 см. Знайдіть площу осьового перерізу циліндра, описаного навколо даної призми.

Ответы

Автор ответа: Iife20

Объяснение:

№1

Позначемо вершини осьового перерізу АВСД, а вершини призми КМЕ і К₁М₁Е₁, центр кола циліндра О і О₁. Осьовий переріз – це прямокутник, а діагональ АС ділить його на 2 рівні прямокутні трикутники АВС і САД. Розглянемо ∆АСД. В ньому АД і СД – катети, а АС – гіпотенуза. Катети АД також є діаметром циліндра. Знайдемо АД через косинус кута. Косинус кута – це відношення прилеглого до кута катета до гіпотенузи, тому:

cosСАД=АД/АС →

→ АД=АС×cosСАД=12×cos30°=12×√3/2=

=12√3/2=6√3см.

Якщо діаметр АД=6√3см, то R=АО=ОД=АД÷2=6√3÷2=3√3см.

Основою правильної трикутної призми є правильний трикутник, в якого всі сторони та кути рівні. Знайдемо сторону цвєї основи, користуючись формулою знаходження радіуса описанного кола:

R=a/√3, де а=КЕ – сторона основи.

КЕ=КМ=МЕ=К₁М=М₁Е=К₁Е₁=R×√3=3√3×√3==3×3=9см.

Бічне ребро призми дорівнює висоті циліндра, тому:

АВ=СД=КК₁=ММ₁=ЕЕ₁.

З ∆АСД знайдемо висоту призми, яка також є висотою циліндра за теоремою Піфагора:

АС²=АД²+СД² →

→ СД²=АС²–АД²=12²–(6√3)²=144–36×3=

=144–108=36;

СД=АВ=КК₁=ММ₁=ЕЕ₁=√36=6см.

Так як призма прямокутна та правильна, то всі ії бічні грані рівні, тоді знайдемо площу однієї грані, наприклад КК₁Е₁Е:

Sгр=КЕ×КК₁=9×6=54см².

Так як всього граней 3, знайдемо площу бічної поверхні. Площа бічної поверхні – це сума всіх бічних граней призми:

Sб.=Skk₁e₁e+Skk₁m₁m₁+Smm₁e₁e

Sб.=54×3=162см²

ВІДПОВІДЬ: Sб.=162см².

№2

Позначемо вершини осьового перерізу АВСД, вершини призми КМЕ і К₁М₁Е₁, висоту основи МН, а центр кола циліндра О і О₁. Основою правильної трикутної призми є правильний трикутник, в якого всі сторони і кути рівні. Знайдемо сторону трикутника за формулою висоти:

МН=КЕ×√3/2

добуток середніх членів пропорції дорівнює добутку крайніх:

КЕ×√3=2×МН

КЕ×√3=2×9

КЕ=18/√3.

КЕ=КМ=МЕ=К₁М=М₁Е=К₁Е₁=18/√3см.

Знайдемо радіус описаного кола за формулою:

R=a/√3, де а – КЕ – це сторона основи.

R=АО=ОД=АД÷2=18/√3÷√3=

=18/√3×1/√3=18÷3=6см.