Question

Знайдіть об'єм тіла, отриманого обертанням вказаних ліній x=y^2. y=x, навколо осі ox

Answer 1

Ответ:

Пошаговое объяснение:

Формула для расчета объема тела вращения вокруг оси ОХ

$\displaystyle V=\pi \int\limits^b_a {y^2(x)} \, dx$

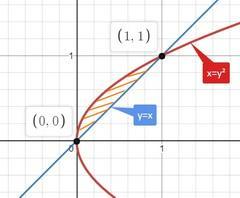
Выполним построение тела вращения

Найдем точки пересечения графиков

$\displaystyle \left \{ {{x=y^2} \atop {y=x}} \right.$

Решив систему получим точки пересечения графиков О(0; 0), A(1;1)

Тогда пределы интегрирования для нас будут a = 0; b = 1.

Искомый объем представляет собой разность объема V₁ параболоида, образованного вращением кривой х=у², и о объема V₂ конуса, образованного вращением прямой y = x.

$\displaystyle V=\pi \int\limits^1_0 {(x-x^2)} \, dx= \pi \bigg(\frac{x^2}{2} \bigg |_0^1-\frac{x^3}{3} \bigg |_0^1\bigg )=\frac{1}{2} \pi -\frac{1}{3} \pi =\frac{1}{6} \pi$