Предмет: Математика,
автор: agunda12
Доказать справедливость равенства
Приложения:
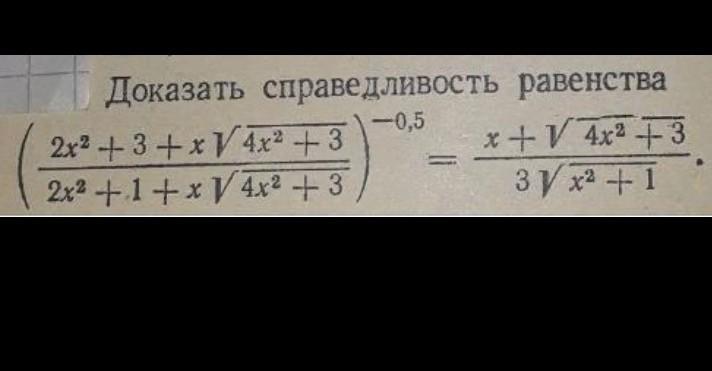
Ответы
Автор ответа:
2
Похожие вопросы
Предмет: Русский язык,
автор: максим826
Предмет: Қазақ тiлi,
автор: Амир261
Предмет: Русский язык,
автор: кукурузка5
Предмет: Математика,
автор: dimacelujkin
Предмет: Русский язык,
автор: vivtash2005