Предмет: Математика,
автор: pandusus04
Помогите решить предел методом Лопиталя, пожалуйста)
Прикрепил скрин
Приложения:
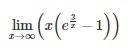
Ответы
Автор ответа:
0
; Получили неопределенность вида
. Осталось заметить, что
и
дифференцируемы, скажем, в окрестности
, ни в какой точке этой окрестности бесконечности функция
не обращается в нуль, а предел
существует и равен
. Следовательно, этому же значению равен и исходный предел (по теореме Лопиталя).
Похожие вопросы
Предмет: Русский язык,
автор: полина856
Предмет: Русский язык,
автор: venera2563
Предмет: Русский язык,
автор: zolotuhinaoksi
Предмет: Математика,
автор: ravan928
Предмет: Обществознание,
автор: ЕгоКотейшество