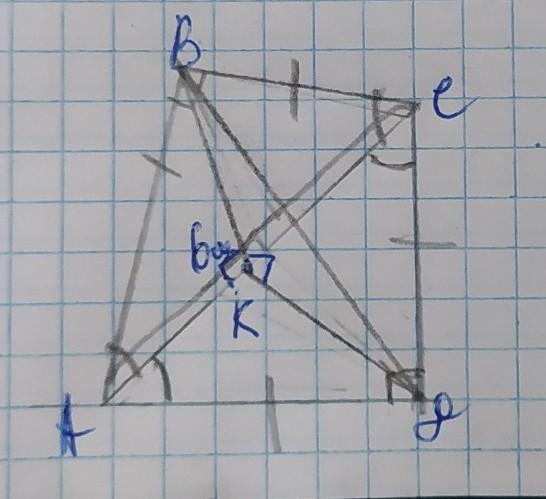
Рівнобедрені прямокутні трикутники ABC i ADC мають
спільну гіпотенузу AC завдовжки 6 см, а їхні площини перпен-
дикулярні . Знайдіть відстань між точками В i D.
Ответы
Ответ:
ВД=3√2см
Объяснение:
У равнобедренных прямоугольных треугольников острые углы равны по 45°, поэтому ∠ВАС=∠ВСА=∠САД=∠АСД=45°. У треугольников АВС и АВД острые углы по 45° и общая гипотенуза АС=6см, значит треугольники равны по 4-му признаку – гипотенузе и острому углу, тогда АВ=ВС=АД=СД. При этом АС является основанием в обоих треугольниках. Проведём высоты ВК и ДК к гипотенузе АС. Так как треугольники равнобедренные, то высота, опущенная к основанию является ещё биссектрисой и медианой. Так как треугольники равны, то их медианы также будут равны. Медиана прямоугольного треугольника, проведённая из вершины прямого угла к гипотенузе равна её половине, тогда ВК=ДК=АС÷2=6÷2=3см.
∆ВДК – прямоугольный, (по условию, так как плоскости треугольников перпендикулярны), где ВК и ДК – катеты, а ВД – гипотенуза. Найдём ВД по теореме Пифагора:
ВД²=ВК²+ДК²=3²+3²=9+9=18
ВД=√18=3√2см.
Можно найти другим способом. В равнобедренном прямоугольном треугольнике гипотенуза больше катета в √2 раз, тогда ВД=3√2см