Предмет: Математика,
автор: baisultanovalikhan11
sqrt(2 - sqrt(x + 2)) = x
Приложения:
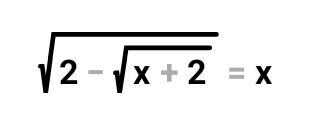
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
Разложим
Произведение равно нулю когда один из множителей равен 0:
Корень 2 посторонний
Корень -1 посторонний
Корень подходит
Остальные посторонние
Похожие вопросы
Предмет: Другие предметы,
автор: filin2323
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: NIKI220577
Предмет: Алгебра,
автор: МиледиТ
Предмет: Русский язык,
автор: ravza52