Предмет: Математика,
автор: qgx7sbh5vg
-
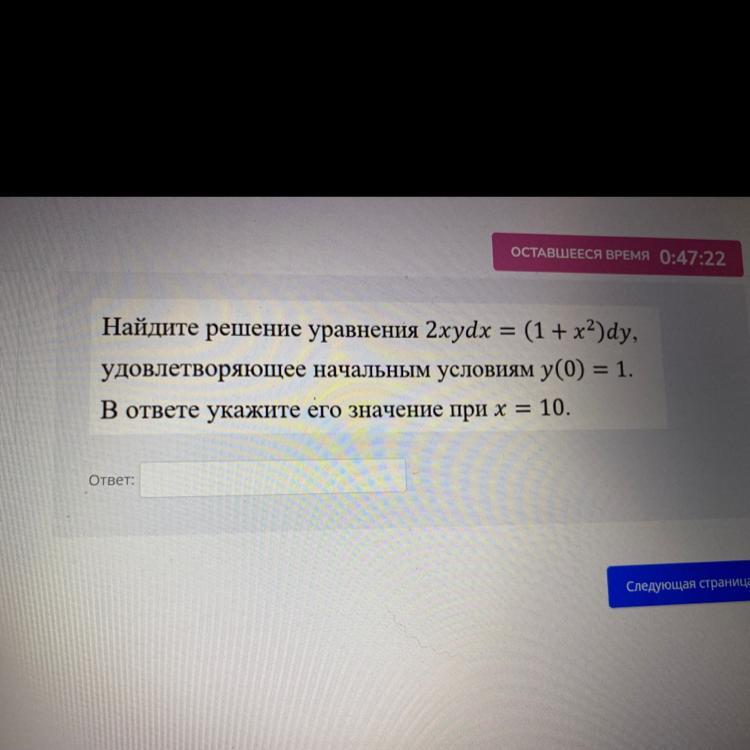
Найдите решение уравнения
Приложения:
natalijawirt:
101
Ответы
Автор ответа:
2
Ответ:
101
Пошаговое объяснение:
Интегрируем
Для удобства пишем свободный член
Экспоненцируем
Решаем задачу Коши : y(0)=1
Решение:
__
Значение при х=10:
Похожие вопросы
Предмет: Английский язык,
автор: annapavA
Предмет: Қазақ тiлi,
автор: валеруська1
Предмет: Русский язык,
автор: kimz
Предмет: Русский язык,
автор: Tatyana20060405
Предмет: Геометрия,
автор: KoToBoY