Очень срочно. Даю 100 б. Постройте график функции (см. ниже)
И определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
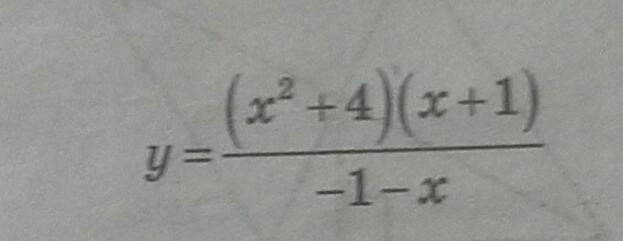
Ответы
Ответ:
В решении.
Объяснение:
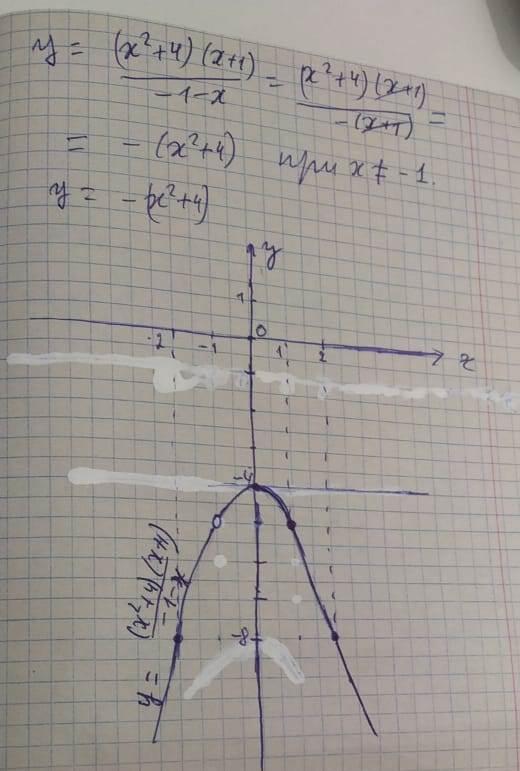
1) Постройте график функции у = ((x²+4)*(x+1))/(-1-x).
Преобразовать уравнение для упрощения:
((x² + 4)*(x + 1))/(-1 - x) = ((x² + 4)*(x + 1))/ -(1 + x) =
Сократить числитель и знаменатель на (х + 1);
= (х² + 4)/ (-1) = -х² - 4;
у = -х² - 4;
Уравнение квадратичной функции, график - парабола со смещённым центром, ветви направлены вниз.
ОДЗ: х ≠ -1 (при этом значении х знаменатель дроби равен нулю, функция не определена).
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -2 -1 0 1 2
у -8 -5 -4 -5 -8
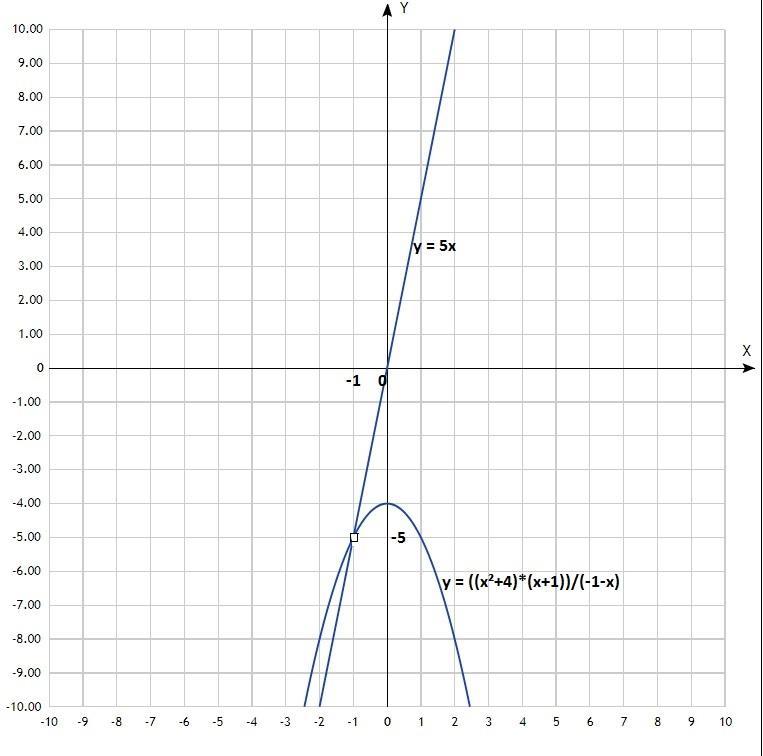
Следует иметь ввиду, что график хоть и строится по вычисленным точкам, точка с координатами (-1; -5) является "выколотой", функция в этой точке не существует.
2) Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Прямая y = kx имеет с графиком ровно одну общую точку, если проходит через указанную "выколотую" точку.
Найти уравнение этой прямой.
Вычислить значение k. Для этого в уравнение подставить известные значения х и у (координаты "выколотой" точки):
y = kx
-5 = k * (-1)
-5 = -k
k = 5;
Уравнение прямой:
у = 5х;
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. График - прямая линия, проходящая через начало координат.
Таблица:
х -1 0 1
у -5 0 5
При k = 5 прямая y = kx имеет с графиком ровно одну общую точку.
Ответ:
Объяснение
Так как ОДЗ: х≠-1,то
при х≠-1, получим
Для того,чтобы парабола y=-(x^2+4) и прямая y=kx имело ровно одну общую точку, необходимо, чтобы дискриминант уравнения -(x^2+4)=kx был равен нулю.
-(x^2+4)=kx
-(x^2+4)-kx=0
x^2+4+kx=0
x^2+kx+4=0
D=k²-4×1×4=k²-16
k²-16=0⇒k=±4
При k=-4 -(x^2+4)=-4x⇒x^2+4=4x; x^2+4-4x =0⇒(х-2)²=0 ⇒х=2 ≠-1
При k=4 -(x^2+4)=4x⇒x^2+4=-4x; x^2+4+4x=0⇒(х+2)²=0 ⇒х=-2 ≠-1
Ответ:При к=±4