Предмет: Алгебра,
автор: Аноним
Производная Помогите пожалуйста
Приложения:
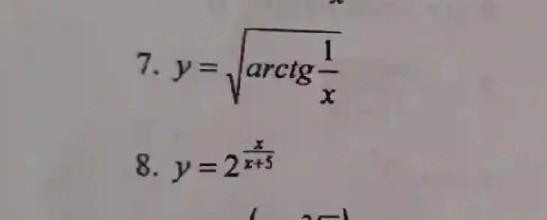
Ответы
Автор ответа:
1
Ответ:
Пользуемся правилом нахождения производной сложной функции.
Похожие вопросы
Предмет: Английский язык,
автор: radgan
Предмет: Английский язык,
автор: dashasolop2002dasha
Предмет: Русский язык,
автор: AlexeyKot
Предмет: Русский язык,
автор: Danalife
Предмет: Биология,
автор: saneksuper2006