Question

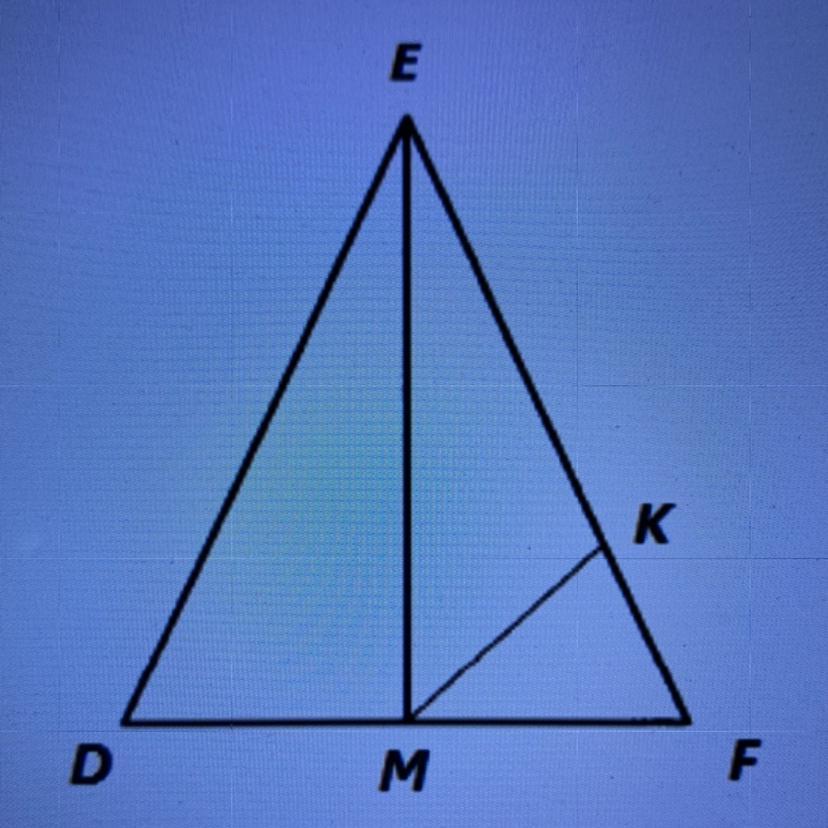
DE=EF и DM=MF

MK- биссектриса треугольника MEF

Найдите угол DMK

Answer 1

Ответ:

135

Объяснение:

Так как DE=EF, значит, наш треугольник равнобедренный

Если DM=MF, то EM - медиана, но в равнобедренном треугольнике она ещё и высота и биссектриса, следовательно, угол EMF прямой, а так как МК - биссектриса, то угол делится на два равных по 45°.

То есть: угол DME = 90°, угол ЕМК = 45°, следовательно, угол DМК равен 135°

Answer 2

ответ:

∠DMK = 135°

объяснение:

по условию DE = EF, значит △DEF равнобедренный. следовательно, высота ЕМ делит треугольник пополам, ∠DME = ∠EMF = 90°.

биссектриса - делит угол треугольника пополам, значит что ∠EMK = ∠KMF = 45°

∠DMK = ∠DME + ∠EMK = 90° + 45° = 135°