Предмет: Математика,
автор: djastinajane
Помогите найти неопределенный интеграл:
∫ ln |tg2x| / cos^2(2x)
Приложения:
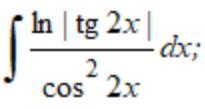
Аноним:
модуль в числителе ?
да
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Формула интегрирования по частям:
Дан неопределенный интеграл
1) Заменим переменную: y=tg2x. Так как
то получим
2) Применим формулу интегрирования по частям. Положим
u=lny, dv=dy.
Отсюда
Тогда
3) Сделаем обратную замену:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Українська мова,
автор: Sergeyburyak82
Предмет: Русский язык,
автор: крутой144
Предмет: Геометрия,
автор: jfhfhhfhgghghfb
Предмет: Литература,
автор: bayezitov