Question

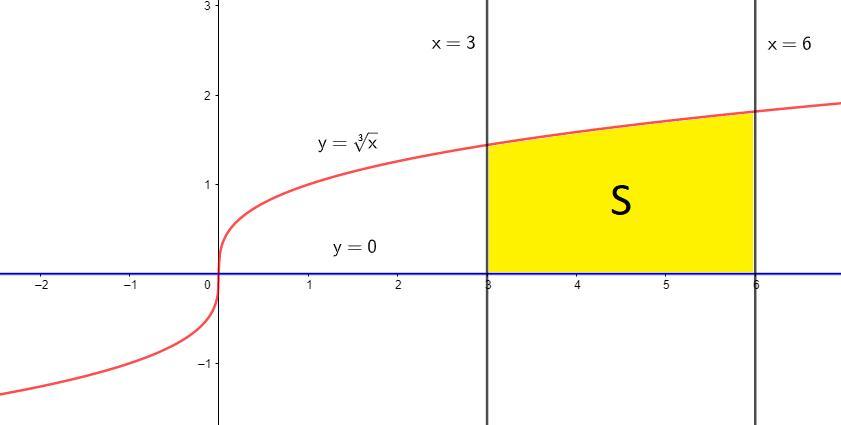
Знайдіть площу криволінійної трапеції, обмеженої лініями y=∛x, x1=3, x2=6, y=0

Answer 1

Ответ:

$\boxed{S= \dfrac{9( 2\sqrt[3]{6} - \sqrt[3]{3} )}{4} }$ квадратных единиц

Объяснение:

По условию фигура ограничена линиями:

$y = \sqrt[3]{x}$

$y = 0$

$x = 3$

$x = 6$

Пределы интегрирования:

$a = 3$

$b = 6$

Найдем площадь криволинейной трапеции по определению:

$S = \displaystyle \int\limits^6_3 {\sqrt[3]{x} } \, dx = \dfrac{3x\sqrt[3]{x}}{4} \bigg |_3^6 = \dfrac{3}{4}(3\sqrt[3]{3} - 6\sqrt[3]{6}) = \dfrac{9( 2\sqrt[3]{6} - \sqrt[3]{3} )}{4}$квадратных единиц