Предмет: Алгебра,
автор: koreaismylove2100
Объясните пожалуйста как это решить. Алгебра, логарифмы.
Приложения:

Ответы
Автор ответа:
0
Ответ:
Объяснение:
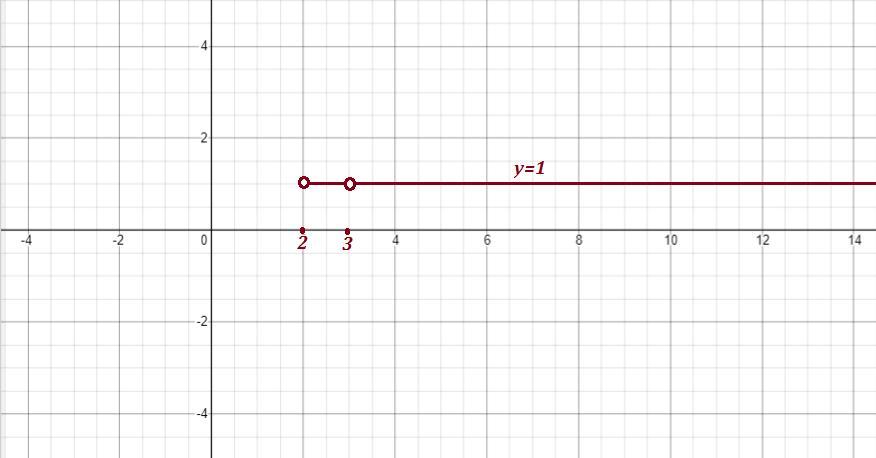
y=log5 (5log(x-2) (x-2))=log5 5=1, y=1 - это прямая, параллельная оси ОХ
и проходящая через точку 1 на оси ОУ, но x-2>0 u x-2 не =1, т.е.
x>2 u x не = 3, о____о_______ , так будет выглядеть график с вы колотыми точками х=2 и х=3 , луч от точки х=2 вправо
Автор ответа:
1
Ответ:
Упростим выражение, применяя свойства логарифмов:
То есть задана функция при
.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: проастронгм
Предмет: Русский язык,
автор: ЧеловекЗ
Предмет: Українська мова,
автор: dubrovinserzh
Предмет: Обществознание,
автор: sharshukovauly