Предмет: Математика,
автор: fdjjsjsjJdjdjdjd
Найти расстояние от точки M до прямой
Приложения:
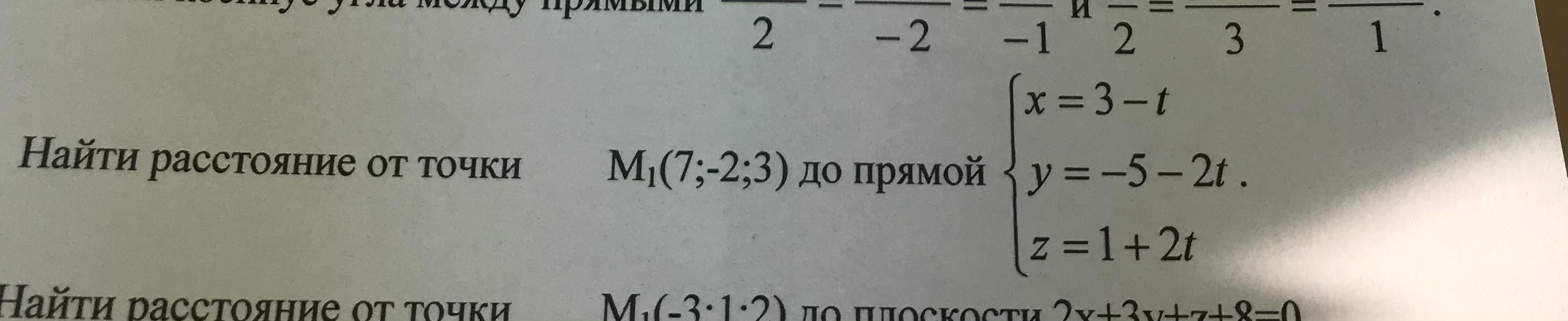
Ответы
Автор ответа:
0
Ответ: d=3 .
Из уравнения прямой находим координаты точки, ей принадлежащей, и координаты направляющего вектора:
Формула расстояния: .
Похожие вопросы
Предмет: Другие предметы,
автор: Аноним
Предмет: Українська мова,
автор: natasemyanik
Предмет: Русский язык,
автор: korolStanislav
Предмет: Литература,
автор: YliaRey