Предмет: Алгебра,
автор: zajnetdinovsultan3
........................
Приложения:

Ответы
Автор ответа:
2
Ответ:
Объяснение:
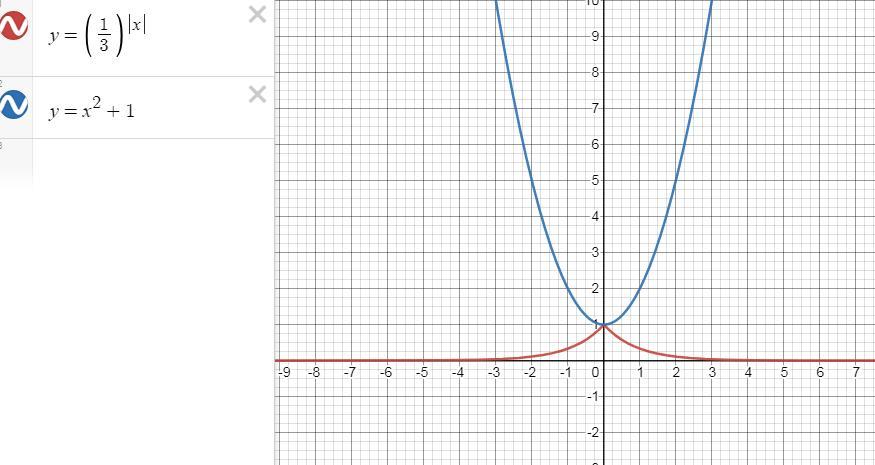
рассмотрим наше неравенство
справа парабола, минимальное значение равно 1
слева показательная функция с основанием 0<1/3<1
ее показатель в модуле
если x<0, то слева функция будет возрастать и наибольшее ее значение будет при х=0 равно
если x<0 , то убывать
поэтому наибольшее значение
равно 1
значит,
неравенство верно для всех х
Ответ:
графики это подтверждают
Приложения:
Похожие вопросы
Предмет: Українська література,
автор: свввв
Предмет: Русский язык,
автор: madamnakvasina
Предмет: Русский язык,
автор: vrinka
Предмет: Математика,
автор: duvekemoel
Предмет: Химия,
автор: НастишьКрутышь