Предмет: Алгебра,
автор: solka0000
встановити тип кривої ,знайти центр або вершину і ексцентриситет x^2+4y+6x+5=0
Ответы
Автор ответа:
1
Ответ:
Объяснение:
x²+6x+9-9+4y+5=0
(x+3)²+4y-4=0
(x+3)²+4(y-1)=0
x'=x+3
y'=y-1
y'=-1\4x'²
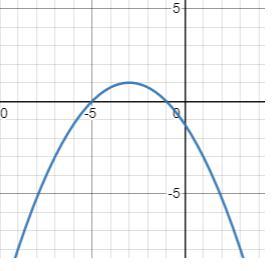
парабола, вершина (-3,1), е=1
Приложения:
Автор ответа:
1
Ответ:
Выделим полный квадрат
Так как переменная "у" в первой степени, а переменная "х" во второй степени, то это уравнение параболы .
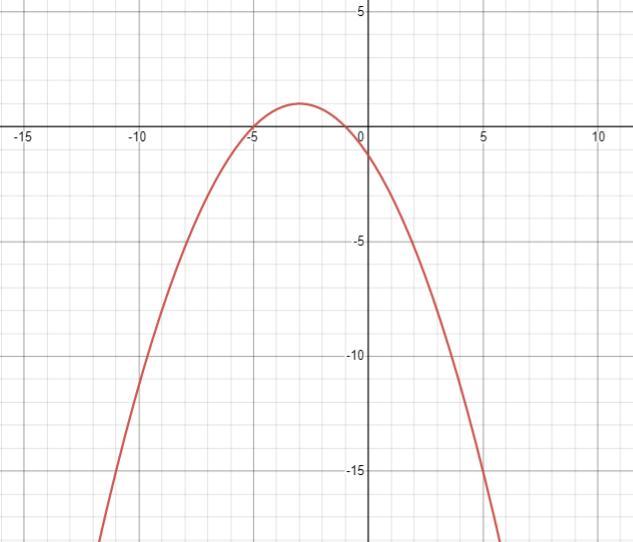
Из уравнения параболы определяем, что вершина параболы находится в точке ( -3; 1 ) . Ось симметрии имеет уравнение х= -3 .
Ветви параболы направлены вниз , так как имеем коэффициент (-1/4) .
Эксцентриситет параболы равен 1 .
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: ibragishka2008
Предмет: История,
автор: kk0792696