Question

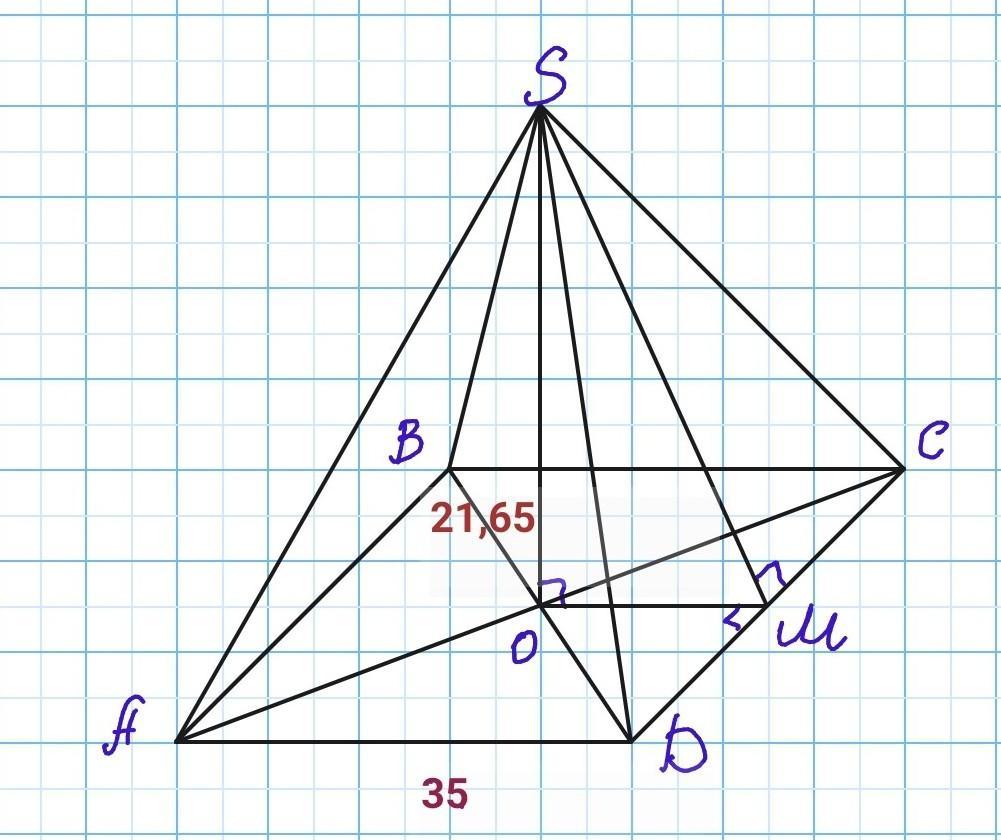
Большая пирамида Лувра в Париже имеет форму правильной четырехугольной пирамиды высотой 21,65 м и длиной стороны основания 35 м.

Answer 1

Ответ:

апофема равна 27,84 м

Площадь стеклянной поверхности пирамиды = 1948,8 м

Объяснение:

Площадь стеклянной поверхности пирамиды = площади боковой поверхности и вычисляется по формуле: 

Sбок = 1/2×L×P

где L — апофема пирамиды; P — периметр основания пирамиды.

Периметр основания пирамиды:

Р=4а=4*35=140 м

где а - длина стороны основания.

 Высота боковой грани правильной пирамиды называется апофемой

О - точка пересечения диагоналей основания. Приведём ОМ перпендикулярно DC.

OM=r=a/2=35/2=17,5 м.

SO ⟂ основанию пирамиды. Значит она перпендикулярна любой прямой принадлежащей основанию. SO⟂ОМ.

По теореме о трёх перпендикулярах SM ⟂ DC => SM- апофема.

Найдём апофему из прямоугольного треугольника SMO по теореме Пифагора:

$SM = \sqrt{ {SO}^{2} + {OM}^{2} } = \sqrt{ {21.65}^{2} + {17.5}^{2} } = \\ \\ = \sqrt{468.72 + 306.25} = \sqrt{774.97} = 27.838$

L=SM≈ 27,84 м

Площадь боковой поверхности:

$S = \dfrac{1}{2} \times 27.84 \times 140 = 1948.8$

Площадь стеклянной поверхности пирамиды = 1948,8 м