Question

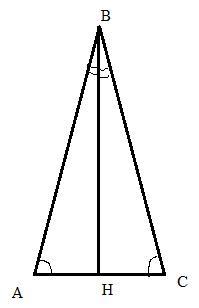
У трикутнику АВС сторони кути ВАС = кут ВСА, а ВН - бісектриса. Доведіть, що трикутники АВН і СВН рівні.

Answer 1

Ответ:

Я так понимаю, что нужно доказать без использования свойств равнобедренных треугольников.

Объяснение:

В треугольниках △АВН и △СВН <BAH=<BCH по условию, а так как ВН - биссектриса, то <ABH=<CBH.

Поскольку сумма углов треугольника 180°, значит и третьи углы этих треугольников также равны между собой <AHB=<CHB.

BH - общая сторона этих треугольников, значит, учитывая, что <ABH=<CBH и <AHB=<CHB, то △АВН=△СВН по 2му признаку.