Предмет: Математика,
автор: vkinsta13
помогите пожалуйста, кто шарит
Приложения:
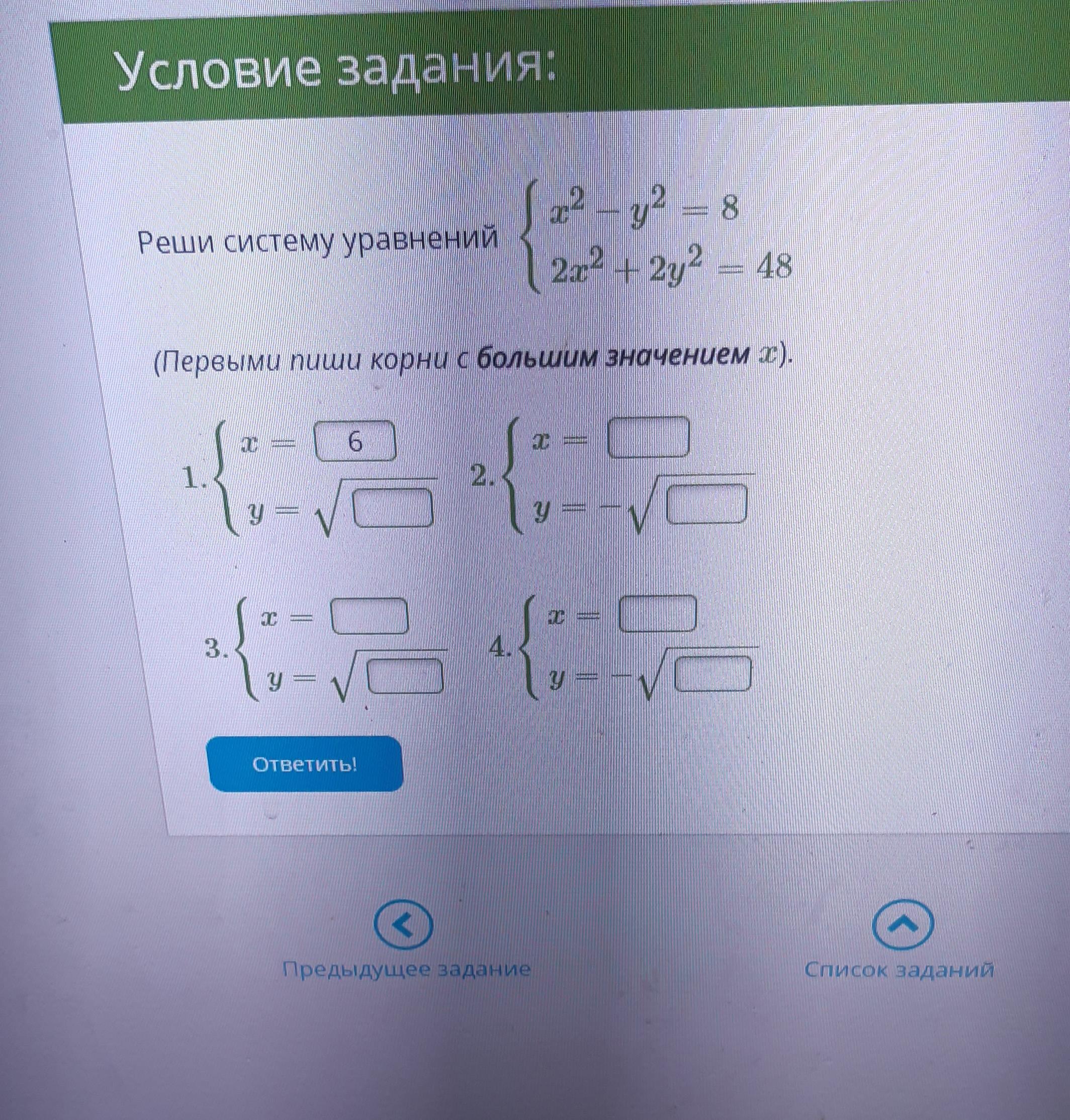
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Тогда система имеет четыре решения
Похожие вопросы
Предмет: Русский язык,
автор: ариана60
Предмет: Русский язык,
автор: лиза3004
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: ispantoza
Предмет: Немецкий язык,
автор: Аноним