Предмет: Математика,
автор: harafgt
Помогите пж!!! Решить систему уравнения!!!
Приложения:
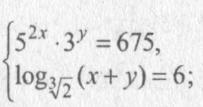
Ответы
Автор ответа:
1
Ответ:
( 1; 3).
Пошаговое объяснение:
Решим первое уравнение системы
Если х=1 , то y= 4 - 1 = 3.
Тогда ( 1; 3) - решение системы .
Похожие вопросы
Предмет: Английский язык,
автор: tanechkamedved3
Предмет: Русский язык,
автор: goskov2005
Предмет: Русский язык,
автор: ionkina87
Предмет: Алгебра,
автор: Okril
Предмет: Математика,
автор: pavluxi1985