Question

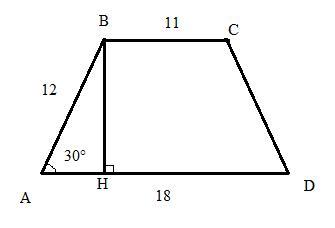
В равнобедренной трапеции угол при основании равен 30 градусов, основания равны 11см и 18см, боковая сторона равна 12см. Найти площадь трапеции. Помогите пожалуйста

Answer 1

Ответ:

Объяснение:

Задача кривая. Слишком много данных, при этом не сходятся 2 различных решения.

Решение 1:

Пусть ВН - высота. Тогда в прямоугольном треугольнике △АВН ВН=(1/2)*АВ=12/2=6см (катет, лежащий против угла в 30°).

S(ABCD)=((AD+BC)/2)*BH=((18+11)/2)*6=87см².

Решение 2:

Основания высот равнобедренной трапеции, опущенных из вершин меньшего основания, делят большее основание на отрезки, один из которых равен меньшему основанию, а два других – полуразности оснований.

То есть АН=(AD-BC)/2=(18-11)/2=3,5см.

Тогда в прямоугольном треугольнике △АВН ВН=√(АВ²-АН²)=√(12²-3,5²)=√131,75см.

S(ABCD)=((AD+BC)/2)*BH=((18+11)/2)*√131,75=166,43см² (примерно)

Рекомендую конечно взять первое решение, но почему они не сходятся - понятия не имею.