Question

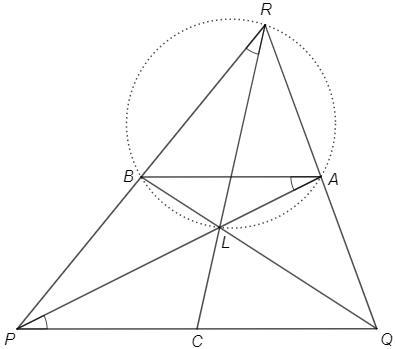
Задание №4. В треугольнике PQR точка L пересечение медиан PA и QВ. Окружность, описанная около треугольника RAB, проходит через точку L. Найдите Длину медианы, проведённой из вершины R, если PQ =18. ​

Answer 1

Угадаем ответ. В равностороннем треугольнике медианы являются высотами, углы PAR и QBR прямые, четырехугольник RALB вписанный, условие задачи выполнено. RC=√3/2 PQ

AB||PQ (средняя линия)

∠BAP=∠APQ (накрест лежащие)

∠BAL=∠BRL (вписанные)

=> ∠LPC=∠PRC

△LPC~△PRC (по двум углам)

PC/RC =LC/PC

PC=PQ/2, LC=RC/3 (медианы делятся 2:1)

=> PQ/2 :RC =RC/3 :PQ/2 => RC =√3/2 PQ =9√3