Предмет: Алгебра,
автор: svetadanilchenkova
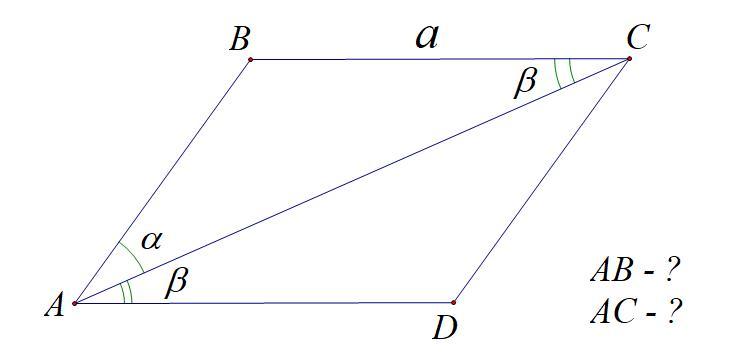
В параллелограмме АВСД сторона ВС равна а,угол ВАС=а,угол САД=В.Найти другую сторону параллелограмма и диагонали АС.
Ответы
Автор ответа:
1
1. ∠CAD = ∠BCA = β (накр. леж. при BC || AD и секущей AC)
2. Рассмотрим ΔABC.
∠A + ∠B + ∠C = 180° ⇒ ∠B = 180° - ∠A - ∠C = 180° - (α + β)
По теореме синусов:
Из первых двух дробей получаем:
Из крайних дробей получаем:
Приложения:
svetadanilchenkova:
Спасибо!
Похожие вопросы
Предмет: Окружающий мир,
автор: зябликДаша
Предмет: Українська мова,
автор: mariyalavrova1
Предмет: Окружающий мир,
автор: Irina19882501
Предмет: Русский язык,
автор: marjapon4ikp825tr
Предмет: Литература,
автор: Grata99145