Предмет: Алгебра,
автор: zajnetdinovsultan3
даю 50 баллов за решение
Приложения:
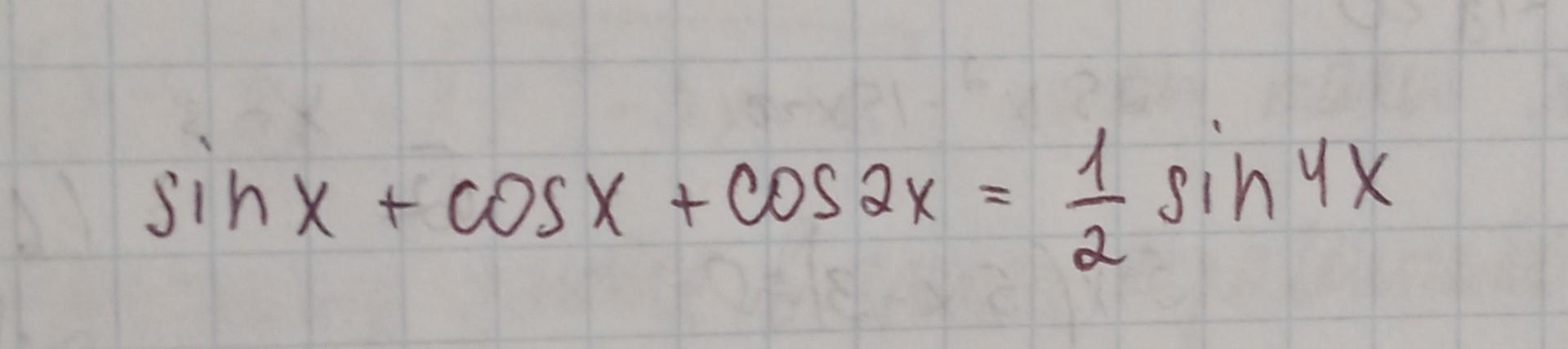
Ответы
Автор ответа:
2
Ответ:
(см. объяснение)
Объяснение:
Перейдем к совокупности:
Для первой строки:
Для второй строки:
Итого:
Уравнение решено!
zajnetdinovsultan3:
Спасибо!
Похожие вопросы
Предмет: Русский язык,
автор: BoIIpoCuku
Предмет: Окружающий мир,
автор: leon123
Предмет: Қазақ тiлi,
автор: nnnn8
Предмет: Математика,
автор: maiermaria20
Предмет: Алгебра,
автор: Kaida2006