найдите сумму всевозможных значений а отражающий сумму корней уравнения
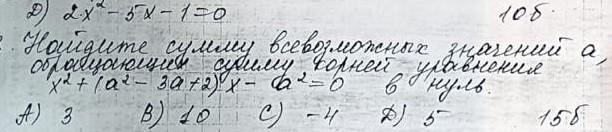
Ответы
x²+(a²-3a+2)х -a²=0
решения уравнения будут существовать, когда
дискриминант D=(a²-3a+2)²+4a²≥0
это выполняется при любых а
Далее,
по т Виета для корней х1 и х2 нашего уравнения
х1+х2=а²-3а+2
по условию задачи
сумма корней =0
то есть :
а²-3а+2=0
(а-1)(а-2)=0
а1=1
а2=2
при этих а
у нас (х1+х2)=0
требуемая сумма всех а: а1+а2= 1+2=3
ответ: А , эта сумма =3
Ответ:
(см. объяснение)
Объяснение:
Первый способ:
Данное уравнение не может не иметь корней.
Запишем теорему Виета для приведенного квадратного уравнения:
По условию сумма корней уравнения равна 0 ().
Тогда верно, что:
Итого, искомая сумма равна .
Второй способ:
Данное уравнение не может не иметь корней.
Решим уравнение относительно .
Пусть . Тогда верно, что:
По условию должно выполняться:
Тогда получим:
Откуда очевиден переход:
Итого, .
Третий способ:
Данное уравнение не может не иметь корней.
Сумма корней уравнения будет равна 0, если координата вершины x параболы равна 0. Воспользуемся формулой .
Тогда получим:
Итого, ответом будет число .
Задание выполнено!