Предмет: Алгебра,
автор: villiwonkka1
49
1 и 2
_._._._._._
Приложения:

Ответы
Автор ответа:
2
Объяснение:
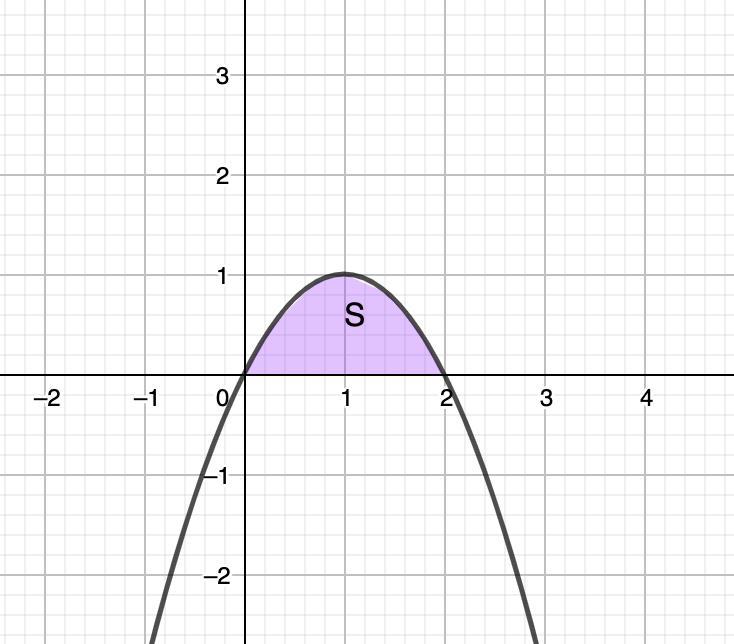
1. Построим график у = -х²+2х
-парабола, ветви вниз.
Точки пересечения с осью 0х:
х = 0; х = 2.
Формула площади фигуры:
У нас:
Найдем площадь:
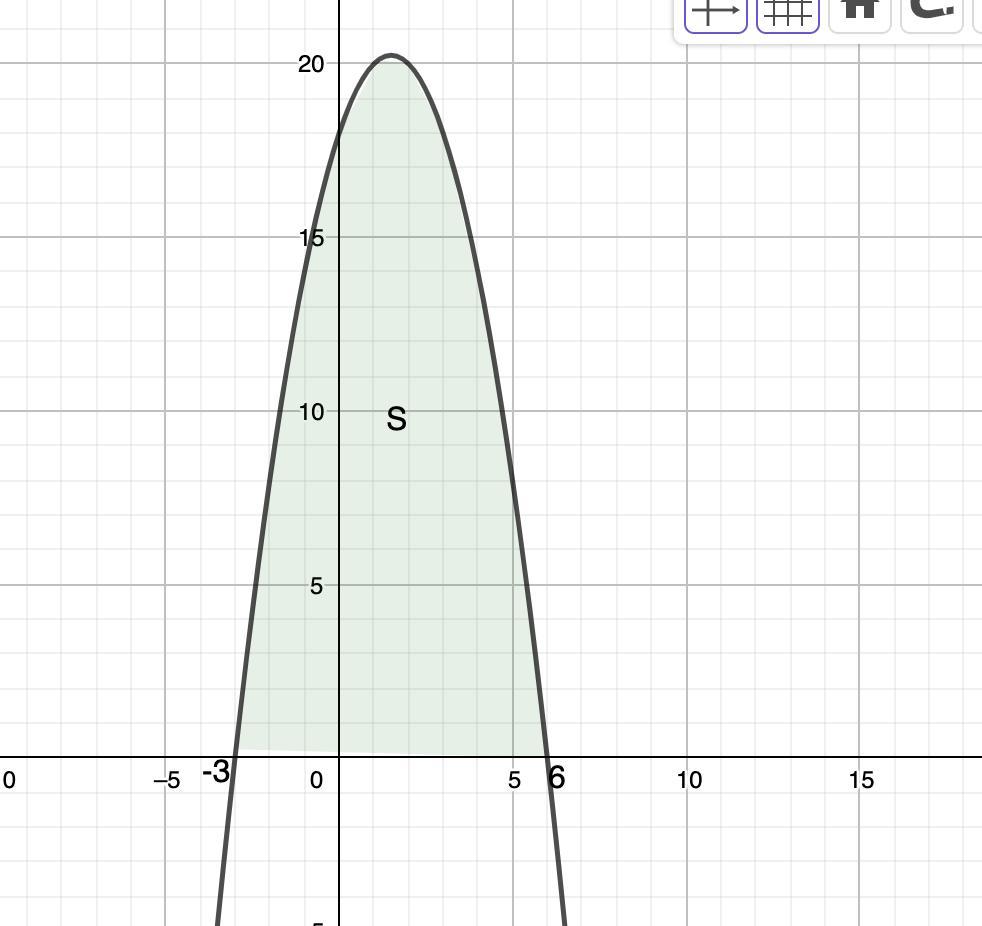
2.
График - парабола, ветви вниз.
Точки пересечения с 0х:
Имеем:
Найдем площадь:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: karolinakrudu
Предмет: Английский язык,
автор: настя200534
Предмет: Окружающий мир,
автор: sashalogvinenco
Предмет: Обществознание,
автор: zakhar200641
Предмет: Геометрия,
автор: sostog