Предмет: Алгебра,
автор: Аноним
Найдите площадь фигуры, ограниченной линиями у=4; у=х^0,5; х=2; х=0. Помогите пожалуйста СРОЧНО !!!!!
Ответы
Автор ответа:
3
Ответ:
квадратных единиц
Объяснение:
По условию фигура ограничена линиями:
Так как график "расположен выше" графика
, а пределы интегрирования от 0 до 2, то:
квадратных единиц.
Приложения:
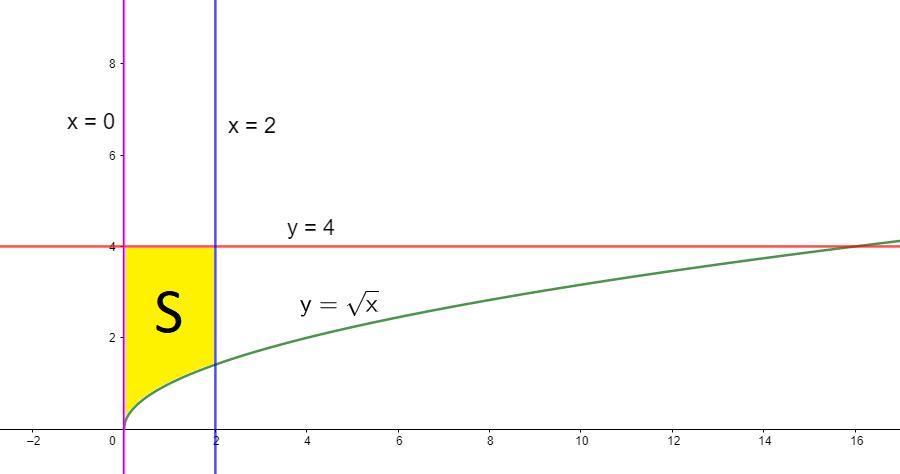
Автор ответа:
4
Ответ:
Объяснение:
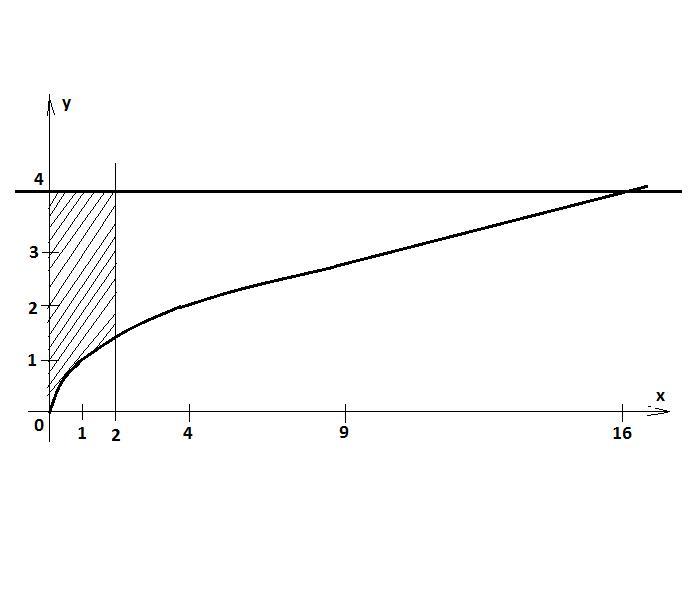
Чертеж прилагается. Площадь равна разности двух интегралов:
Приложения:
спс
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: мати2
Предмет: Физика,
автор: linda698
Предмет: Алгебра,
автор: RikaIslamova
S=\int\limits^2_0 {4} \, dx -\int\limits^2_0 {\sqrt{x} } \, dx =4x|^2_0-\frac{2}{3}*x^{3/2} |^2_0=4*2-0-\frac{2}{3}(\sqrt{2^3} -0)=S=
0
∫
2
4dx−
0
∫
2
x
dx=4x∣
0
2
−
3
2
∗x
3/2
∣
0
2
=4∗2−0−
3
2
(
2
3
−0)=
=8-\frac{2}{3}*2\sqrt{2}=8-\frac{4\sqrt{2} }{3} = 6,1144=8−
3
2
∗2
2
=8−
3
4
2
=6,1144