Question

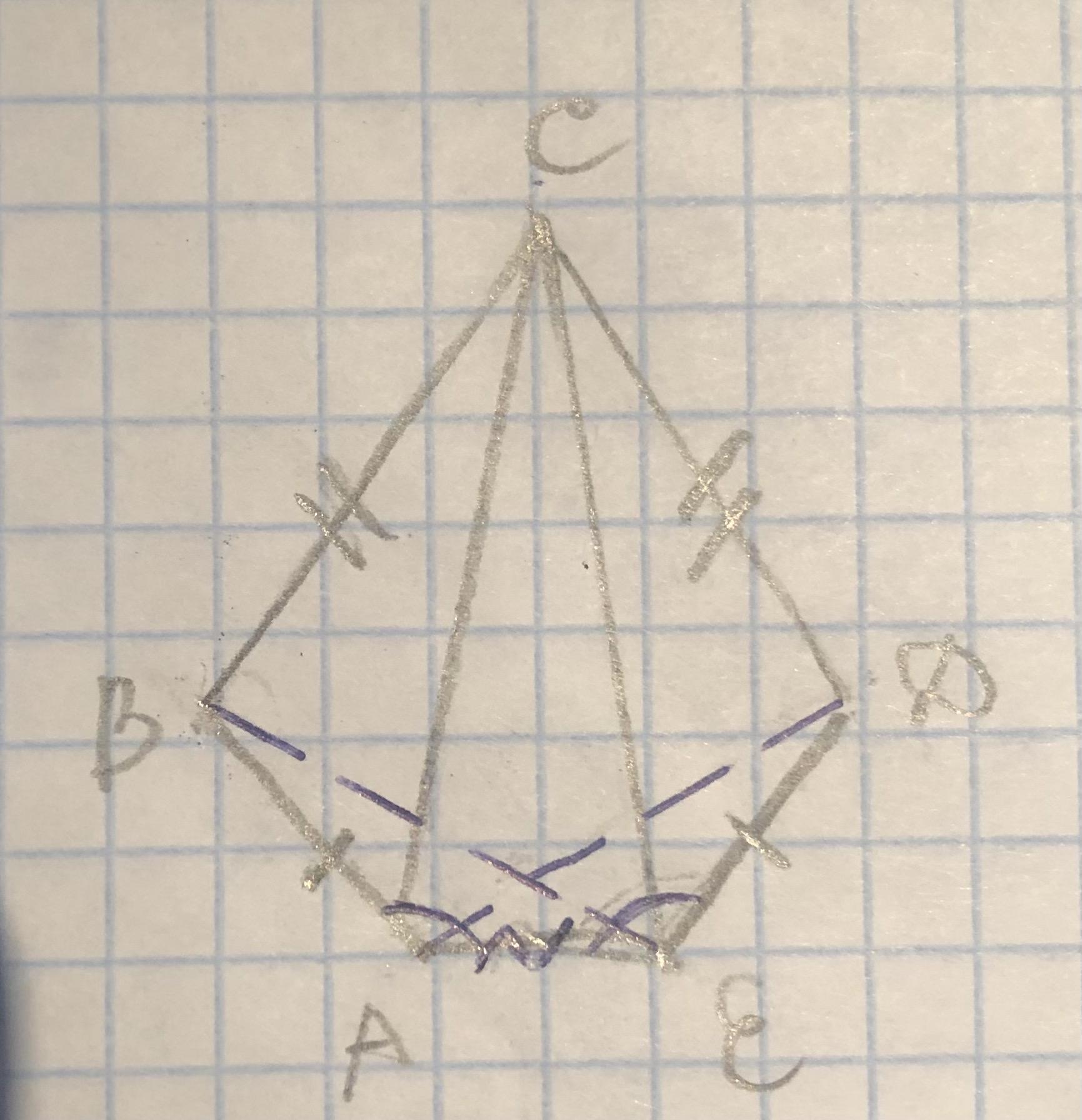
Известно, что LABC = — LEDC = 90° , длины отрезков BC и CD Равны. Докажите Равенство углов ВАС и DEC.
​

Answer 1

Ответ:

чертеж на фото

Объяснение:

1. Доп. построение - соединим точки А и С, Е и С.

2. Рассмотрим треуг. АВС и ЕСД.

ВС=ДС по усл

АВ=ЕД по усл

уг АВС = уг ЕДС по усл

Значит, треуг. АВС= ЕСД по 1 признаку (по двум сторонам и углу между ними).

Из равенства треугольников следует равенство их элементов: нас интересуют стороны АС=ЕС, и углы ВАС=ДЕС

3. Рассмотрим треуг. АСЕ. Он равнобедренный, так как выше доказали, что АС=ЕС. Раз он равнобедренный, то углы при основании равны:

уг САЕ= уг СЕА

4. угол А = углу Е, так как

угол А =уг ВАС +уг САЕ

угол Е =уг ДЕС+уг СЕА

5. Рассмотрим треуг. АВЕ и ЕДА

АВ=ЕД по усл

АЕ - общая сторона

уг А = уг Е из п.4

Значит, треуг. АВЕ= ЕДА по 1 признаку  (по двум сторонам и углу между ними).

Из равенства треугольников следует равенство их элементов: нас интересуют стороны ВЕ=АД, ч.т.д.