Предмет: Алгебра,
автор: ajdarg472
СРОЧНОООООООООООО!!!!!
Приложения:
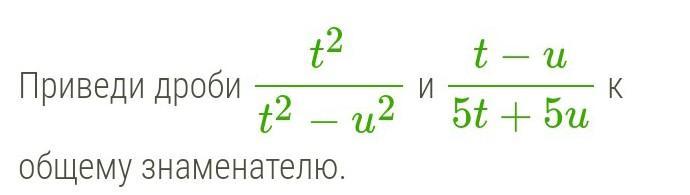
Ответы
Автор ответа:
0
Объяснение:
Разложим каждый знаменатель на множители. В первой дроби применим формулу сокращенного умножения
а во второй вынесем общий множитель 5 за скобки.
Тогда общий знаменатель будет
Дополнительный множитель к первой дроби 5, а ко второй
Похожие вопросы
Предмет: Русский язык,
автор: nastysamok
Предмет: Русский язык,
автор: олеся440
Предмет: Русский язык,
автор: vkovtsur
Предмет: Физика,
автор: Mamadad2513