Предмет: Геометрия,
автор: tamirbalziev228
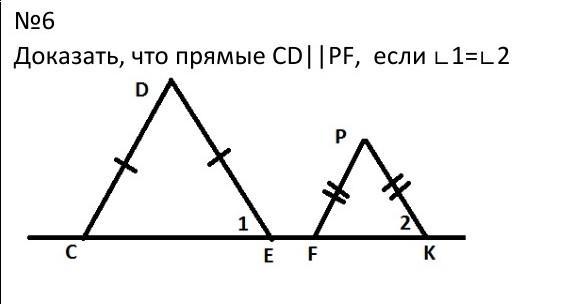
Доказать,что прямые CD | | PF,если угол 1 равен углу 2
Приложения:
Ответы
Автор ответа:
1
- Определение. Треугольник называется равнобедренным, если две его стороны равны.
СD = DE
⇒ ΔСВE - р/б по определению
FP = PK
⇒ ΔFPK - р/б по определению
- Теорема. В равнобедренном треугольнике углы при основании равны.
ΔСВE и ΔFPK - р/б (с основаниями CE и FK соответственно)
∠1 = ∠2 (или ∠DEC = ∠PKF) по условию
⇒ ∠DCE = ∠PFK по свойству р/б треугольника
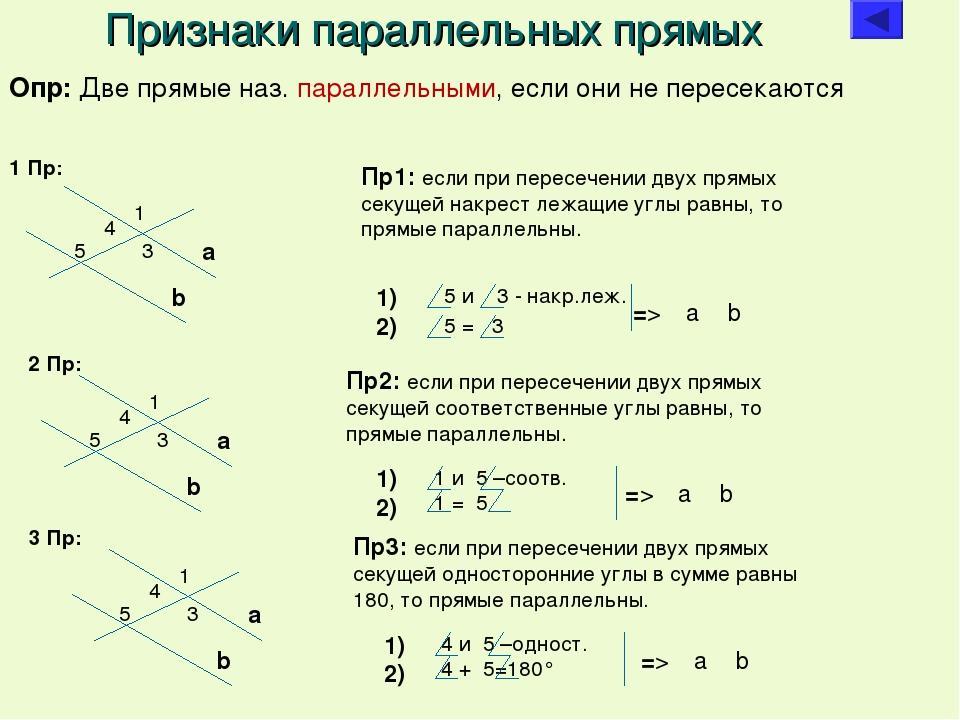
- Теорема. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
∠DCE и ∠PFK - соответственные углы при прямых CD и FK и секущей CK
∠DCE = ∠PFK
⇒ CD ║ PF по II признаку параллельных прямых
Что и требовалось доказать!
Приложения:
tamirbalziev228:
ТЫ КТО ЭНШТЭЙН!?!?!?
Похожие вопросы
Предмет: Русский язык,
автор: ольга12345615
Предмет: Українська мова,
автор: DenMan225
Предмет: Немецкий язык,
автор: Alina240802
Предмет: Английский язык,
автор: zhankamashirova
Предмет: Литература,
автор: amf2011