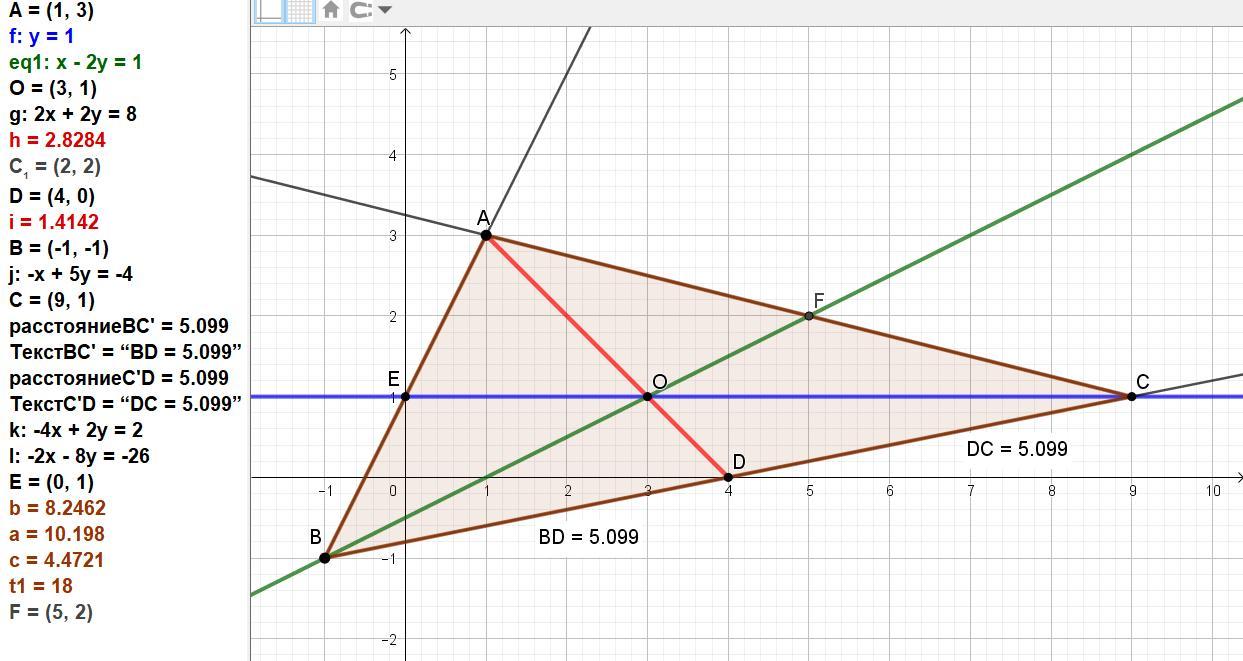
скласти рівняння сторін трикутника, якщо одна з його вершин А (1,3) і рівняння двох його медіана y-1=0 і x-2y=1
Ответы
скласти рівняння сторін трикутника, якщо одна з його вершин А (1,3) і рівняння двох його медіана y-1=0 і x-2y=1.
Находим координаты точки О – точки пересечения медиан, решив систему.
{y-1=0
{x-2y=1. из первого уравнения у = 1 подставим во второе:
х – 2*1 = 1 получаем х = 2 + 1 = 3.
Так как точка О лежит на медиане y-1=0, то её ордината равна 1,Точка О(3; 1).
Далее используем свойство точки пересечения медиан – делить медиану в отношении 2 : 1, считая от вершины.
Δx(OD) = (1/2) Δx(AO) = (1/2)(3-1) = (1/2)*2 = 1. x(D) = x(O) + 1 = 3 + 1 = 4.
Δy(OD) = (1/2) Δy(AO) = (1/2)(1-3) = (1/2)*(-2) = +1. y(D) = y(O) + (-1) = 1 - 1 = 0.
Найдена точка D – основание медианы на стороне ВС.
D(4; 0).
Переходим к точке F. Её ордината равна ((у(А) + у(С)) / 2 = (3 + 1)/2 = 2.
А так как она лежит на прямой х – 2у = 1, то подставим в это уравнение у = 2,
х – 2*2 = 1, отсюда х = 4 + 1 = 5. Точка F(5; 2).
По точке F находим координаты точки С, как симметричной точке А относительно точки F по формуле:
x(C) = 2x(F) – x(A) = 2*5 – 1 = 10 – 1 = 9.
Найдена точка С(9; 1).
По точке D находим координаты точки B, как симметричной точкеC относительно точки D по формуле:
x(B) = 2x(D) – x(C) = 2*4 – 9 = 8 – 9 = -1.
y(B) = 2y(D) – y(C) = 2*0 – 1 = 0 – 1 = -1.
Найдена точка B(-1; -1).
Теперь находим уравнения сторон треугольника по координатам двух точек.
Вектор АВ = (-1-1; -1-3) = (-2; -4).
Уравнение АВ: (x – 1)/(-2) = (y – 3)/(-4) каноническое, или
2x – y + 1 = 0 в общем виде.
Вектор АС = (9-1; 1-3) = (8; -2).
Уравнение АС: (x – 1)/8 = (y – 3)/(-2) каноническое, или
x + 4y - 13 = 0 в общем виде.
Вектор BС = (9-(-1); 1-(-1)) = (10; 2).
Уравнение BС: (x +1)/10 = (y + 1)/2 каноническое, или
x - 5y - 4 = 0 в общем виде.