Отдам 100 баллов, если кто то сможет решить. Помогите пж
Найти приближенное значение функции:
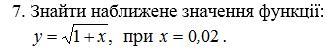
Ответы
Ответ:
Вариант 1. Найдем приближенное значение функции у = √(1+0,02) с двумя знаками после запятой.
Оценим подкоренное выражение 1,02 сначала в целых числах. Так как 1 < 1,02 < 4, то √1 < √1,02 < √4 или 1 < √1,02 < 2. Поэтому десятичная запись числа √1,02 начинается с цифры 1, т. е. √1,02 ≈ 1.
Найдем теперь цифру десятых. Для этого будем возводить в квадрат десятичные дроби 1,1; 1,2; 1,3… до тех пор, пока вновь не оценим такими числами подкоренное выражение 1,02. Имеем 1,12 = 1,21; Так как 1 < 1,01 < 1,1 или 12 < 1,02 < 1,12, то 1 < √1,02 < 1,1. Значит, √1,02 ≈ 1,1.
Чтобы найти цифру сотых, будем последовательно возводить в квадрат десятичные дроби 1,01; 1,02, вновь оценивая подкоренное выражение 1,02. Имеем: 1,01² = 1,0201, что больше, чем 1,02, но очень близко к этому значению, √1,02 ≈ 1,01.
Аналогично проверяем значение подкоренного выражения при значении корня 1,0099. Имеем: 1,0099² = 1,0199, что меньше, чем 1,02, но очень близко к этому значению, поэтому с точностью до двух знаков √1,02 ≈ 1,01.
Если нужна большая точность, то надо проделать аналогичные вычисления при значениях корня в промежутке 1,0099 и 1,01.
С точностью до пятого знака получаем корень, равный 1,00995.
Вариант 2.
Древние вавилоняне пользовались следующим способом нахождения приближенного значения квадратного корня их числа х. Число х они представляли в виде суммы а² +b, где а² ближайший к числу х точный квадрат натурального числа а, и пользовались формулой :
√(a² + b) ≈ a + (b/2a).
Получим √(1² + 0,02) ≈ 1 + (0,02/2*1) = 1,01.
Вариант 3.
Исаак Ньютон разработал метод извлечения квадратного корня, который восходил еще к Герону Александрийскому (около 100 г. н.э.). Метод этот (известный как метод Ньютона) заключается в следующем.
Пусть а1 — первое приближение числа √x (в качестве а1 можно брать значения квадратного корня из натурального числа — точного квадрата, не превосходящего х) .
Следующее, более точное приближение а2 числа √x найдется по формуле
a_2=1/2 (a_1+x/a_1 ).
Третье, еще более точное приближение a_3=1/2 (a_2+x/a_2 ) и так далее.
(n+1)-е приближение √x найдется по формуле a_(n+1)=1/2 (a_n+x/a_n ).
Нахождение приближенного значения числа√1,02 методом Ньютона дает следующие результаты: а1=1; а2= 1,01; а3=1,00995.
Вариант 4.
С использованием формулы для приближенного вычисления с помощью дифференциала:
f(xo+∆x)=f(xo)+d[f(xo)]
На первом этапе необходимо составить функцию f(xo) . По условию предложено вычислить корень из числа: √1,02 , поэтому соответствующая функция имеет вид:f(x)=√x . Нам нужно с помощью формулы найти приближенное значение f(1,02)=√1,02 .
В качестве xo подбираем «хорошее» значение, чтобы корень извлекался нацело. Естественно, это значение xo должно быть как можно ближе к 1.02. В данном случае: xo =1. Действительно: √1=1.
Если xo =1 , то приращение аргумента: ∆x=0,02.
Итак, число 1,02 представлено в виде суммы xo+∆x=1+0,02.
Далее работаем с правой частью формулы
f(xo+∆x)=f(xo)+d[f(xo)] .
Сначала вычислим значение функции в точке xo =1. Собственно, это уже сделано ранее: f(xo)=f(1)=√1=1
Дифференциал в точке находится по формуле: d[f(xo)]=f^' (xo)*∆x.
Из формулы следует, что нужно взять первую производную:
f' (x)=(√x)'=(x^(1/2) )^'=1/2 x^(-1/2)=1/(2√x)
И найти её значение в точке xo:
f^' (xo)=f^' (1)=1/(2√1)=1/2.
Таким образом: d[f(1)]=f^' (1)*∆x=1/2*0,02=0,01
Согласно формуле получаем значение f(1,02) = 1+0,01 = 1,01.
Найденное приближенное значение достаточно близко к более точному значению 1,00995.