Question

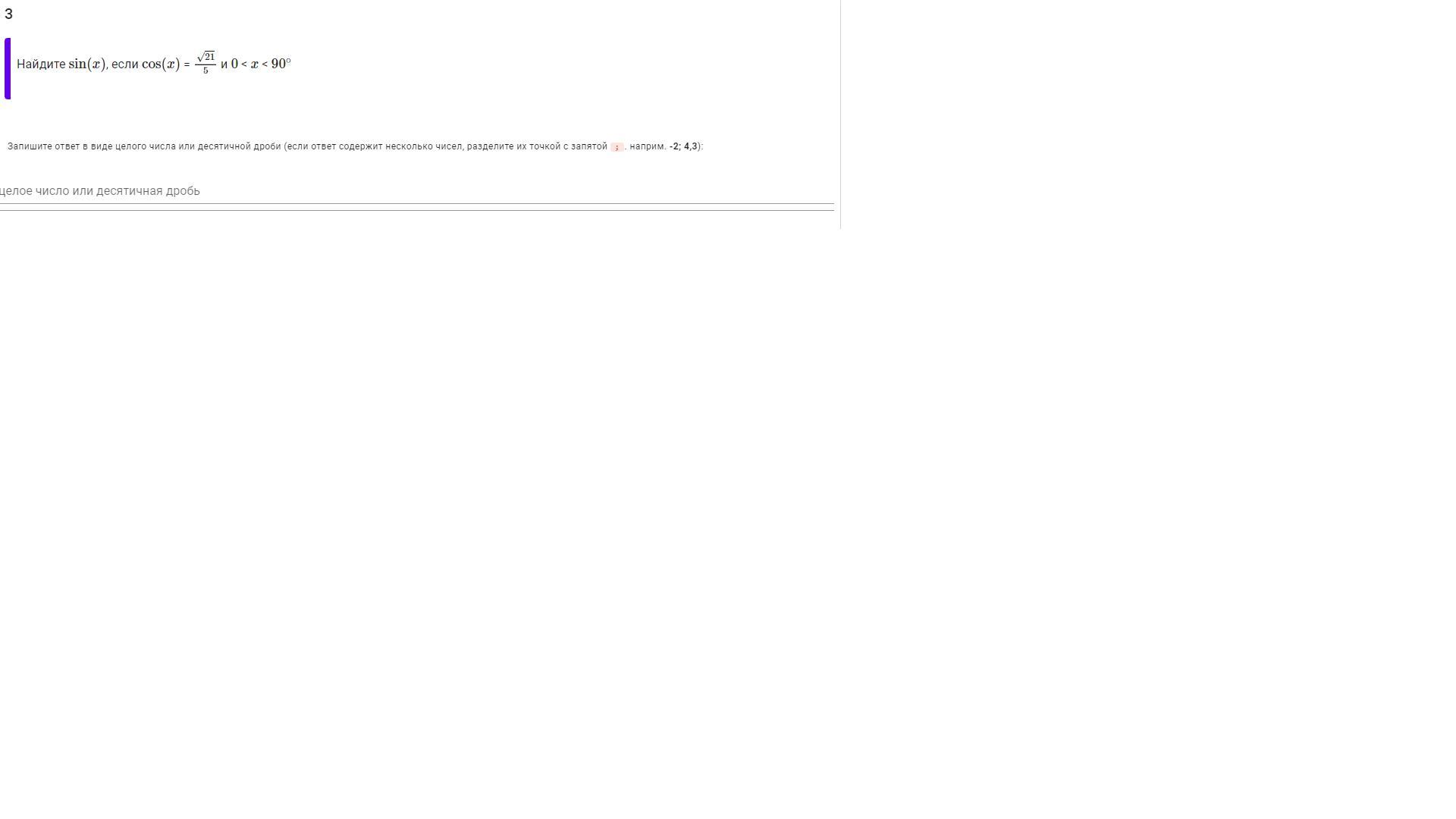
Найдите sin(x), если

Answer 1

Ответ:

Объяснение:

sinx=$\sqrt{1-cos^{2}x } =\sqrt{1-\frac{21}{25} } =\frac{2}{5}$

Синус в первой четверти положителен

Answer 2

Ответ:

sin x=0,4

Объяснение:

${0}^{0} < x < {90}^{0} \\ cosx = \frac{ \sqrt{21} }{5}$

основное тригонометрическое тождество:

${sin}^{2} x + {cos}^{2} x = 1 \\ {sin}^{2} x = 1 - {cos}^{2} x \\ sinx = - + \sqrt{1 - {( \frac{ \sqrt{21} }{5})}^{2} } \\ sinx = - + \frac{2}{5}$

по условию известно что 0°<х<90°, => sin x>0

sin x=2/5, sin x=0,4