Нужна помощь, помощникам спасибо!

Ответы
Ответ:
Объяснение:
Ответ на фото
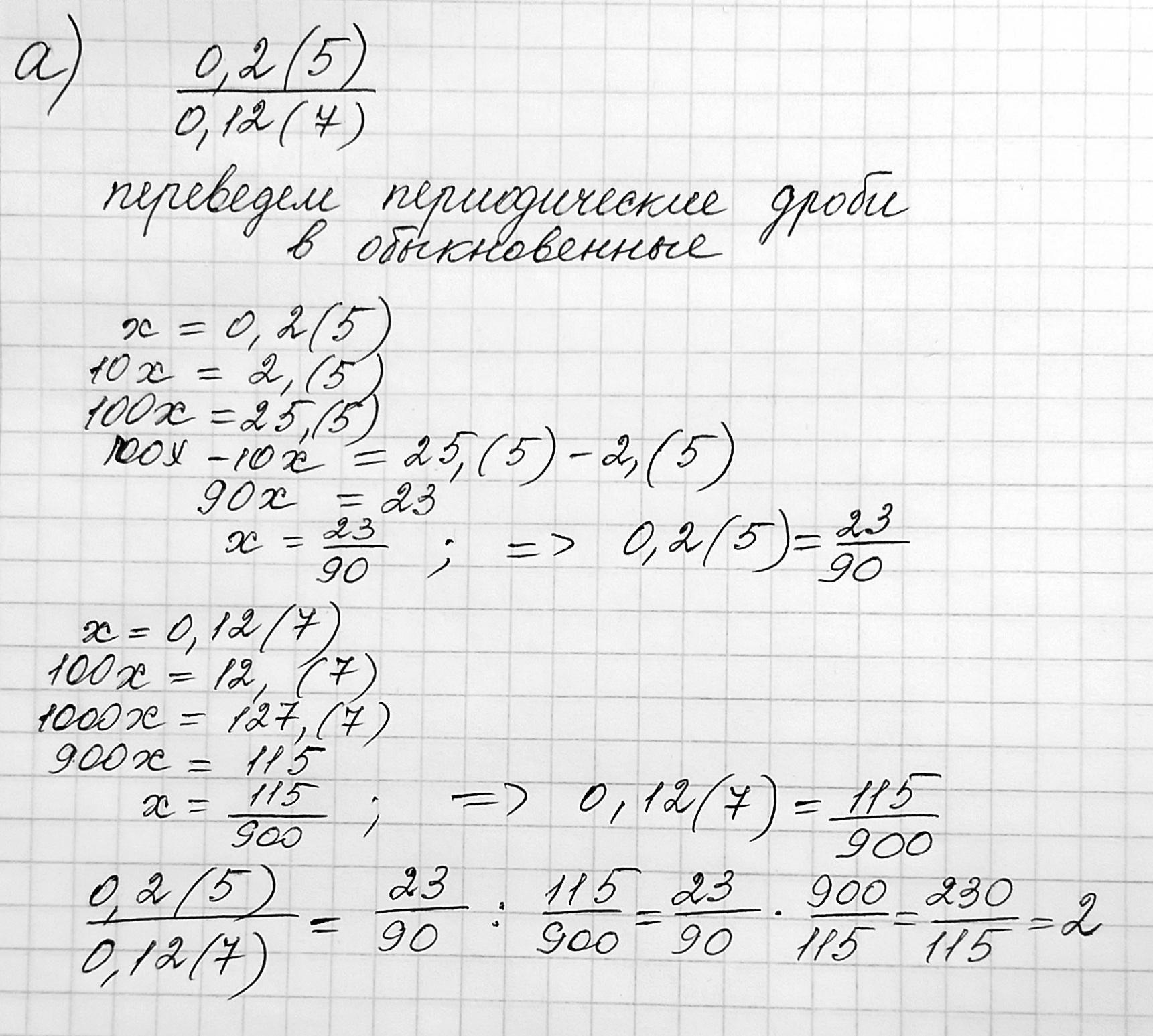

а) 1) вспомним формулу для суммы бесконечно убывающей геометрической прогрессии со знаменателем по модулю меньшим единице.
s=b₁/(1-q),
2) т.к. 0.2(5)=0.2+0.05+0.005+0.0005+..., то для суммы 0.05+0.005+0.0005 эта формула как раз и применима. каждый последующий член здесь в 10 раз меньше предыдущего, значит, q=0.1
s=b₁/(1-q)=0.05/(1-0.1)=5/90; числитель перепишем так
0.2+5/90=2/10+5/90=18/90+5/90=23/90,
3) аналогично поступим со знаменателем дроби.
0.12(7)=0.12+0.007+0.0007+0.00007+...
посчитаем сумму 0.007+0.0007+0.00007+..
s=b₁/(1-q)=0.007/(1-0.1)=7/900; знаменатель дроби перепишем так
0.12+7/900=12/100+7/900=108/900+7/900=115/900=23/180
4) разделим числитель на знаменатель, (23/90):(23/180)=180/90=2
Ответ 2
б) 0.2(27)=0.2+0.027+0.00027+0.0000027+..
0.027+0.00027+0.0000027+..=0.027/(1-0.01)=0.027/0.99=27/990=3/110;
0.2(27)=2/10+3/110=25/110=5/22
0.(63)=0.63+0.0036+0.000063+...=0.63/(1-0.01)=63/99=7/11=14/22
(5/22):(14/22)=5/14
Ответ 5/14