Предмет: Алгебра,
автор: abrikosBobrov
помогите срочн000001
Приложения:
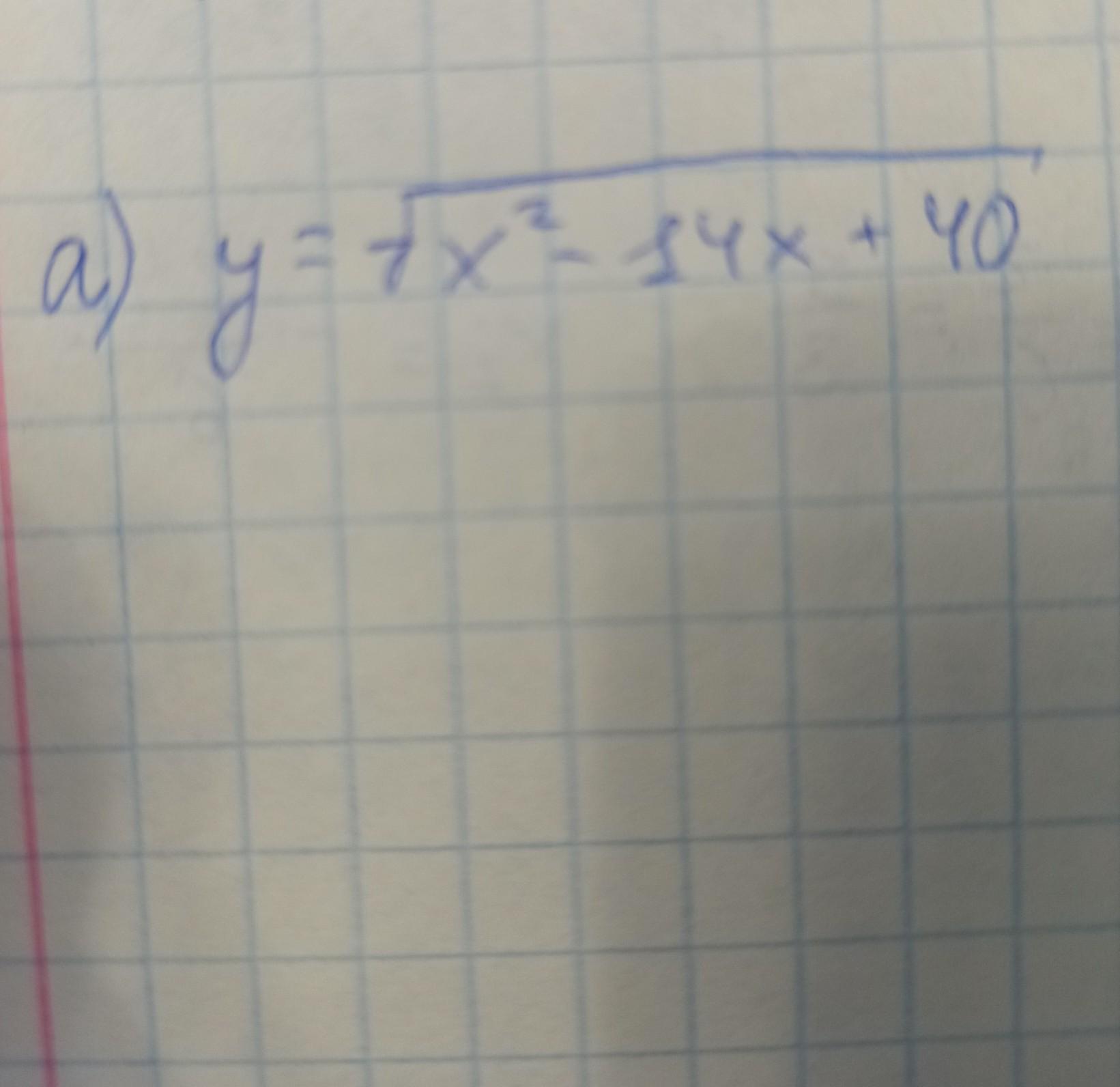
sangers1959:
ОДЗ?
нет, область определения функции
через дискриминант пожалуйста если можешь
Ответы
Автор ответа:
0
Объяснение:
ОДЗ:
-∞__+__4__-__10__+__+∞
Ответ: x∈(-∞;4]U[10;+∞).
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: aliabaimanbetova
Предмет: Русский язык,
автор: maaayan
Предмет: Українська література,
автор: FernandoColins
Предмет: Английский язык,
автор: mia1686
Предмет: Английский язык,
автор: kashtanovaa1998