Question

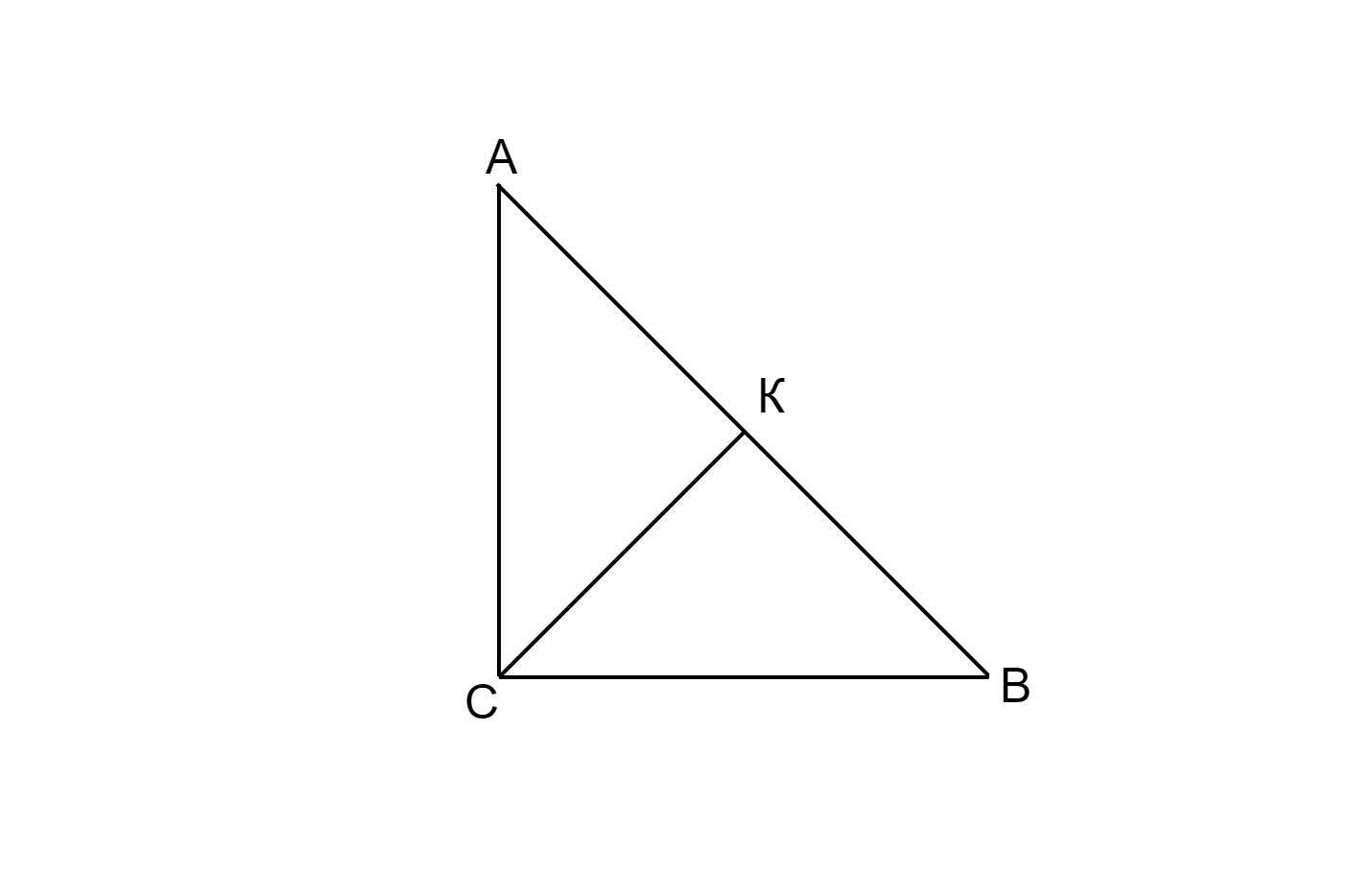
высота CK прямоугольного треугольника ABC проведенная гипотенузе делит её на отрезки длиной 9 см и 25 см Найдите катеты и периметр треугольника.
Помогитеееее​

Answer 1

В прямоугольном треугольнике высота, проведенная к гипотенузе, есть среднее геометрическое между отрезками гипотенузы⇒

h=√(9*25)=3*5=15(см)

ΔАСК , т Пифагора АС=√(15²+9²)=√306 см

ΔВСК, т Пифагора ВС=√(15²+25²)=√850см

Р=(9+25)+√306+√850=34+3√34+5√34=34+8√34

Answer 2

Ответ:

$\: AC{=}3 \sqrt{34} \: cm;\:BC{ =}5 \sqrt{34}\: cm; \:\\ P_{ \triangle{ABC}}=34{+}8\sqrt{34}\: cm$

Объяснение:

Дано:

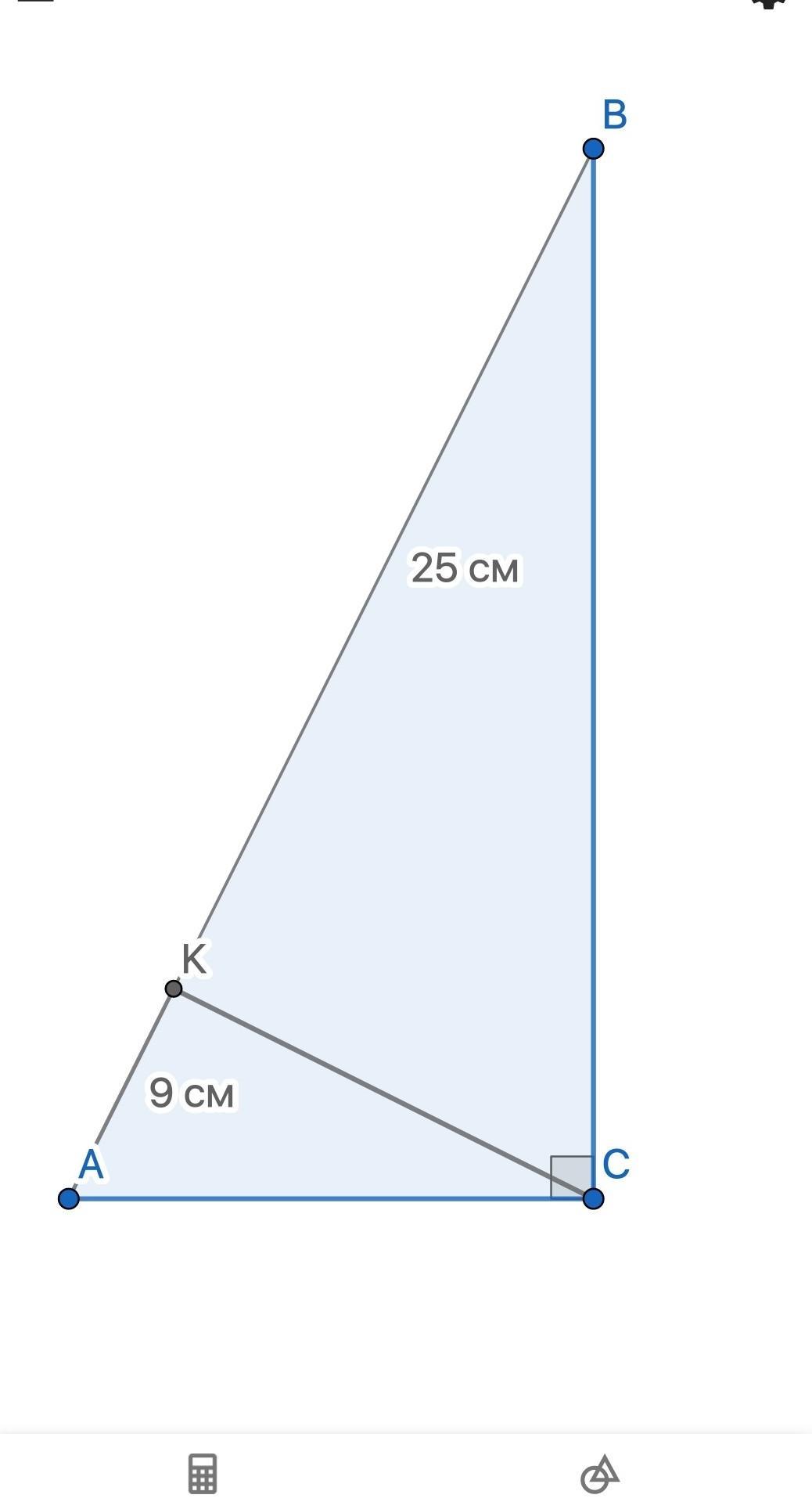
∆АВС, уг.С = 90°

СК _|_ АВ; АК = 9 см; ВК = 25 см

Найти:

АС, ВС, Р(∆АВС) - ?

Решение:

т.к. в ∆АВС угол С прямой, то:

$\angle{A} = 180\degree{ - }90\degree {-} \angle{B} =90\degree - \angle{B} \: \\ \angle{B} = 180\degree{ - }90\degree {-} {\angle}{A} =90\degree - \angle{A}$

Рассмотрим ∆АСК и ∆ВСК:

т.к. СК _|_ АВ, =>

$\angle{AKC} = \angle{CKB}= 90\degree$

$\angle{CBK} =180\degree- 90\degree-\angle{B}=90\degree-\angle{B}\\=>\: \: \angle{CBK}=\angle{A} \\ \\ \angle{ACK} = 180\degree-90\degree- \angle{A}=90\degree-\angle{A}\\ =>\:\: \angle{ACK} =\angle{B}$

Следовательно ∆АСК и ∆СВК - подобны,

и соответственно:

$\frac{CK}{AK} = \frac{BK}{CK} \: < = > \:{CK}^{2} = {AK} \cdot{BK} \\ {CK} = \sqrt{{AK} \cdot{BK}} = \sqrt{9 \cdot25 \: } = 3 \cdot5 = 15 \: cm$

Далее по Т. Пифагора найдем стороны АС и ВС:

$AC^2{=} AK^2{+}KC^2\:\: =>\:\: AC{ =}\sqrt{AK^2{+}KC^2}\\AC{ =}\ \sqrt{ {9}^{2} { +} {15}^{2} }{ = } \sqrt{81 {+ }225} { = } \sqrt{306}{ = } \\ = \sqrt{9{ \cdot}34} = 3 \sqrt{34} \: cm \\ \\BC^2{= }BK^2{+}KC^2\:\: =>\:\: BC{ =}\sqrt{BK^2{+}KC^2}\\BC{ =}\ \sqrt{ {25}^{2} { +} {15}^{2} }{ = } \sqrt{625 {+ }225} { = } \sqrt{850}{ = } \\ = \sqrt{25{ \cdot}34} = 5\sqrt{34} \: cm$

А длина стороны АВ равна сумме длин ее частей:

$AB = AK+BK \: \: \quad \\ AB= 9+25=34cm$

Найдем периметр ∆АВС:

$P_{ \triangle{ABC}}=AB+BC+AC \\ P_{ \triangle{ABC}}=34+5 \sqrt{34} +3 \sqrt{34} = \\ = 34+(5{ + }3) \sqrt{34} =34{+}8\sqrt{34}$

Итак:

Ответ:

$\: AC{=}3 \sqrt{34} \: cm;\:BC{ =}5 \sqrt{34}\: cm; \:\\ P_{ \triangle{ABC}}=34{+}8\sqrt{34}\: cm$