Предмет: Геометрия,
автор: satesul80
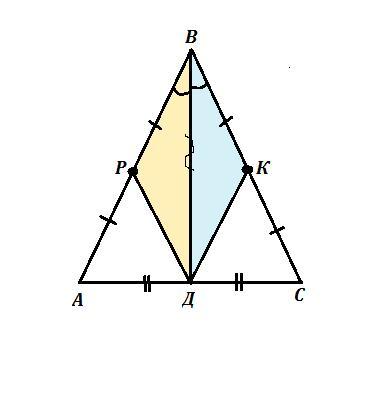
В равнобедренном треугольнике АВС с основанием АС проведена медиана ВD. Точка Р - середина стороны ВА, точка К – середина стороны ВС. Докажите равенство треугольников ВDР и ВDК. Изобразить чертеж.
Ответы
Автор ответа:
0
Ответ:
ΔАВС , АВ=ВС , АР=РВ , ВК=КС .
Так как АВ=ВС , то и половины этих сторон равны между собой: АР=РВ=ВК=КС .
Рассм. ΔВДР и ΔВДС . У них ВР=ВК , ВД - общая сторона и ∠РВД=∠КВД , так как медиана равнобедр. тр-ка , проведённая к основанию, является ещё и биссектрисой .
Значит, ΔВДР=ΔВДС по 1 признаку равенства треугольников .
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: МишинПётр255
Предмет: Русский язык,
автор: svetakirli2002
Предмет: Қазақ тiлi,
автор: Bekzada1990
Предмет: Английский язык,
автор: alsu7691
Предмет: Українська мова,
автор: genka28