Предмет: Математика,
автор: aleksmishkova
Найти предел ( не пользуясь правилом ЛОПИТАЛЯ)
Приложения:
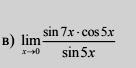
Ответы
Автор ответа:
0
Ответ:
Автор ответа:
0
можно разбить этот предел на произведение пределов двух множителей, а именно
cosx (sin7x/sin5x) , при х стремящемся к нулю cos0=1, домножим числитель на 7/7 и знаменатель оставшегося сомножителя на 5/5 и применим первый замечательный предел дважды, предел отношения синуса игрек к игреку при у стремящемся к нулю, равен единице.
т.е. предел 7(sin7x/7x)/(5*(sin5x/5x)) равен 7*1/(5*1) =1.4
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Аделя71
Предмет: Русский язык,
автор: Nadir005
Предмет: Русский язык,
автор: marisha1213
Предмет: Русский язык,
автор: anya010203
Предмет: Английский язык,
автор: zhibekq212