Question

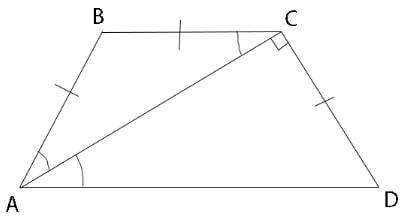
визначити кути рівнобічної трапеції в якій діагональ є бісектрисою гострого кута і перпендикулярна до бічної сторони​

Answer 1

Відповідь:

60°; 120°

Пояснення:

Перш за все визначимо, які кути рівні.

За малюнком видно, що ∠BAC = ∠DAC - кути, утворенні бісектрисою.

∠DAC = ∠BCA - кути при AD ║ BC і січній AC.

∠С = 90° + ∠BAC;

Нехай ∠BAC = α, тоді

∠С = 90° + α;

∠C = ∠ B.

Розглянемо ΔABC:

Сума кутів трикутника дорівнює 180°, тобто:

∠BAC + ∠B + ∠BCA = 180°; Підставляємо:

α + (90° + α) + α = 180°

3α = 90°

α = 30°.

Отже, гострі кути трапеції становлять 2 * α = 2 * 30° = 60°, а тупі - 90° + α = 90° + 30° = 120°