Предмет: Геометрия,
автор: woren
Из вершины прямого угла треугольника проведен перпендикуляр, который делит гипотенузу на отрезки, разность которых равна 21 см. Вычисли гипотенузу треугольника, если длина перпендикуляра равна 10 см.
Ответ:
ПАМАГИИТЕЕЕЕ ПАЖАЛУСТА СРОЧНГОООО!!!!
Ответы
Автор ответа:
0
Ответ:
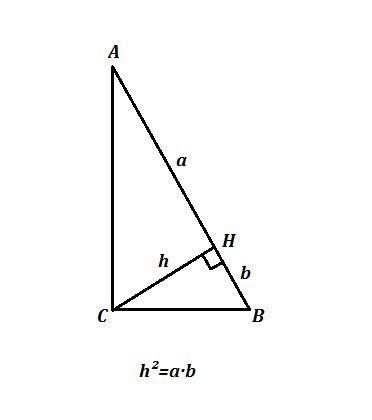
ΔABC , ∠C=90° , AH⊥BC , обозначим h=AH=10 см , AH-BH=a-b=21 см .
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые она делит гипотенузу : h²=ab .
Отрицательное значение b не подходит .
Гипотенуза .
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: semyonzimin
Предмет: Русский язык,
автор: alinagevorgyan
Предмет: Математика,
автор: mamapapa9
Предмет: Математика,
автор: yalovoydanil73