Question

Из вершины прямого угла треугольника проведен перпендикуляр, который делит гипотенузу на отрезки, разность которых равна 21 см. Вычисли гипотенузу треугольника, если длина перпендикуляра равна 10 см.
ПАМАГИИИИТИИИИ

Answer 1

Ответ:

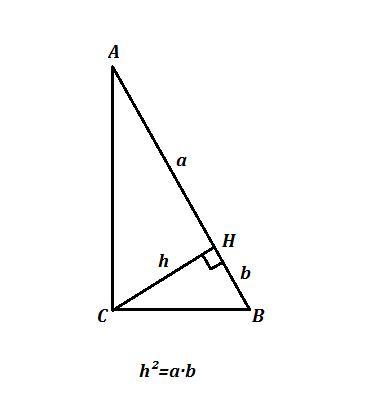
ΔABC ,  ∠C=90° , AH⊥BC ,  обозначим  h=AH=10 см ,  AH-BH=a-b=21 см .

Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые она делит гипотенузу :  h²=ab .

$\left\{\begin{array}{l}10^2=ab\\a-b=21\end{array}\right\ \ \left\{\begin{array}{l}ab=100\\a=b+21\end{array}\right\ \ \left\{\begin{array}{l}(b+21)b=100\\a=b+21\end{array}\right\ \ \left\{\begin{array}{l}b^2+21b-100=0\\a=b+21\end{array}\right$

$b^2+21b-100=0\ \ ,\ \ \ D=21^2+400=831=29^2\ \ ,\ \ b_1=-25\ ,\ b_2=4$

Отрицательное значение b не подходит .

$b=4\ ,\ \ a=4+21=25$

Гипотенуза  $AB=a+b=25+4=29$  .