Предмет: Математика,
автор: vladmarkenco65
Будь ласка допоможіть побратиму
Приложения:

Ответы
Автор ответа:
1
Відповідь:
-9,5
Покрокове пояснення:
P.S Запис має бути як на фото тих двох має бути як на фото
Приложения:
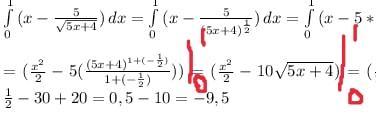
Аноним:
Там пряма палка і над нею 1 а під нею 0
Дякую тобі
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: samsir
Предмет: Українська мова,
автор: kaccya
Предмет: История,
автор: KarolnkaBreivo
Предмет: Алгебра,
автор: mrsirinnikitaa