Question

здравствуйте, у меня возникают большие трудности с задачей 4, можете пожалуйста помощь, желательно на листке

Answer 1

Объяснение:

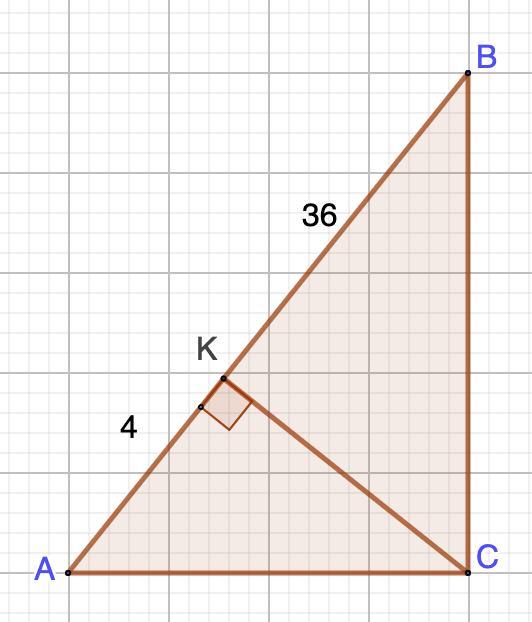
Дано: ΔАВС - прямоугольный.

СК - высота.

АК = 4 см; КВ = 36 см.

Найти: ВС; АС; Р (ΔАВС)

Решение:

• Квадрат катета равен произведению гипотенузы и проекции этого катета на гипотенузу. (Метрические соотношения в прямоугольном треугольнике)

$\displaystyle AC^2=AK*AB\\\\BC^2=BK*AB$

Найдем катеты:

$\displaystyle AC=\sqrt{4*40}=\sqrt{160}=4\sqrt{10}\;_{(CM)}\\\\ BC=\sqrt{36*40}=\sqrt{1440}=12\sqrt{10} \;_{(CM)}$

• Периметр - сумма длин всех сторон треугольника.

Р (ΔАВС) = 4√10 + 12√10 + 40 =( 40 +16√10) (см)