Question

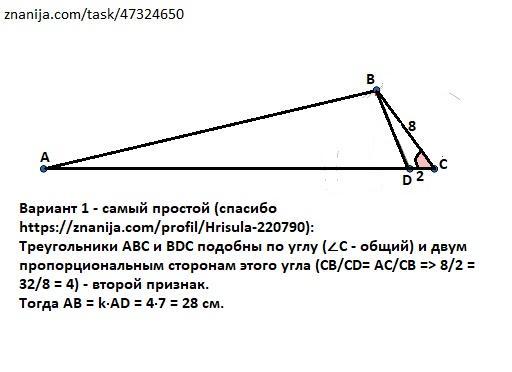
У трикутнику ABC BC=8 см. Точка D належить стороні AC, до того ж CD=2см, AD=30см, BD= 7см. Знайдіть сторону AB.
Помоги пожалуйста ребята ❤️​

Answer 1

Ответ:

АВ = 28 см.

Объяснение:

Вариант 1 - самый простой (спасибо https://znanija.com/profil/Hrisula-220790):

Треугольники АВС и ВDС подобны по углу (∠С - общий) и двум пропорциональным сторонам этого угла (СВ/CD= AC/CB => 8/2 = 32/8 = 4) - второй признак.

Тогда АВ = k·AD = 4·7 = 28 см.

Вариант 2:

Проведем высоту ВН. Пусть СН = х, тогда DH = (х-2).

По Пифагору из прямоугольного треугольника СВН:

ВН² = ВС² - СН² = 64 - х². (1)

По Пифагору из прямоугольного треугольника DВН:

ВН² = ВD² - DН² = 49 - (х-2)². (2)

Приравняем (1) и (2):

64 - х² = 49 - (х-2)²  => 64 =  45 + 4х => x = 19/4 = 4,75

CН = 4,75. =>

АН = АС - СН = 32 - 4,75 = 27,25

ВН = √(64 - х²) = √(64 - 22,5625) = √41,4375.

В прямоугольном треугольнике АВD ао Пифагору

АВ = √(АН²+ВН²) = √(742,5625+41,4375) = √748 = 28см.

Вариант 3:

По теореме косинусов в треугольнике CDB

Cos(∠CDB) =  (7² + 2² - 8²)/(2·7·2) = - 11/28.

Тогда Cos(∠ADB) = 11/28, так как ∠CDB и ∠ADB - смежные, а cos(180-α) = -Cosα.

По теореме косинусов в треугольнике ADB:

AB² = AD²+BD² - 2·AD·BD·Cos(∠ADB) = 900 + 49 - 2·30·7·(11/28).

АВ² = 949-165 = 784.

АВ = √784 = 28 см.