Предмет: Алгебра,
автор: sannyily
Буду сердечно благодарна тому, кто поможет с этим примером
Приложения:
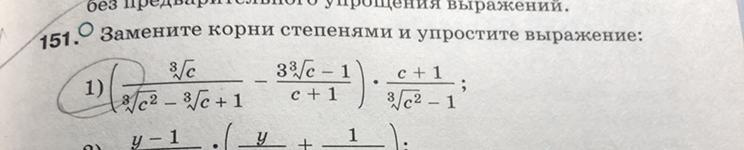
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: chychi
Предмет: Английский язык,
автор: laSkype99
Предмет: Русский язык,
автор: СонькаКарась
Предмет: Математика,
автор: korolek17
Предмет: Математика,
автор: 96780