Предмет: Алгебра,
автор: Давид005234
Вычислите интеграл. 100 балллв
Приложения:
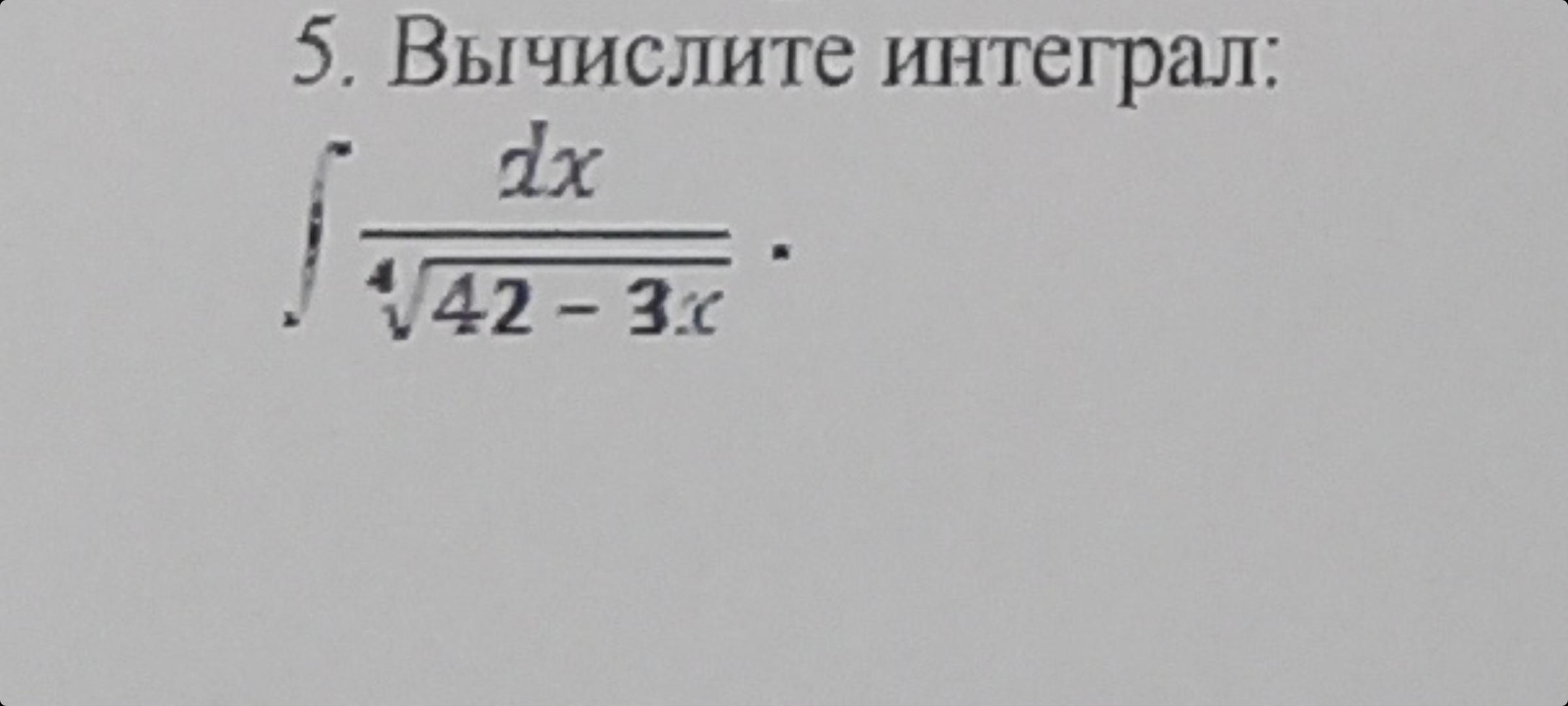
Ответы
Автор ответа:
0
Ответ:
Интегрирование путём подведения под знак дифференциала.
Похожие вопросы
Предмет: Другие предметы,
автор: 23456789vita123
Предмет: Қазақ тiлi,
автор: suleimenovadana1
Предмет: Английский язык,
автор: Аноним
Предмет: Биология,
автор: belozerova1katy
Предмет: Русский язык,
автор: nanasister228