Предмет: Геометрия,
автор: fonarikanarik898
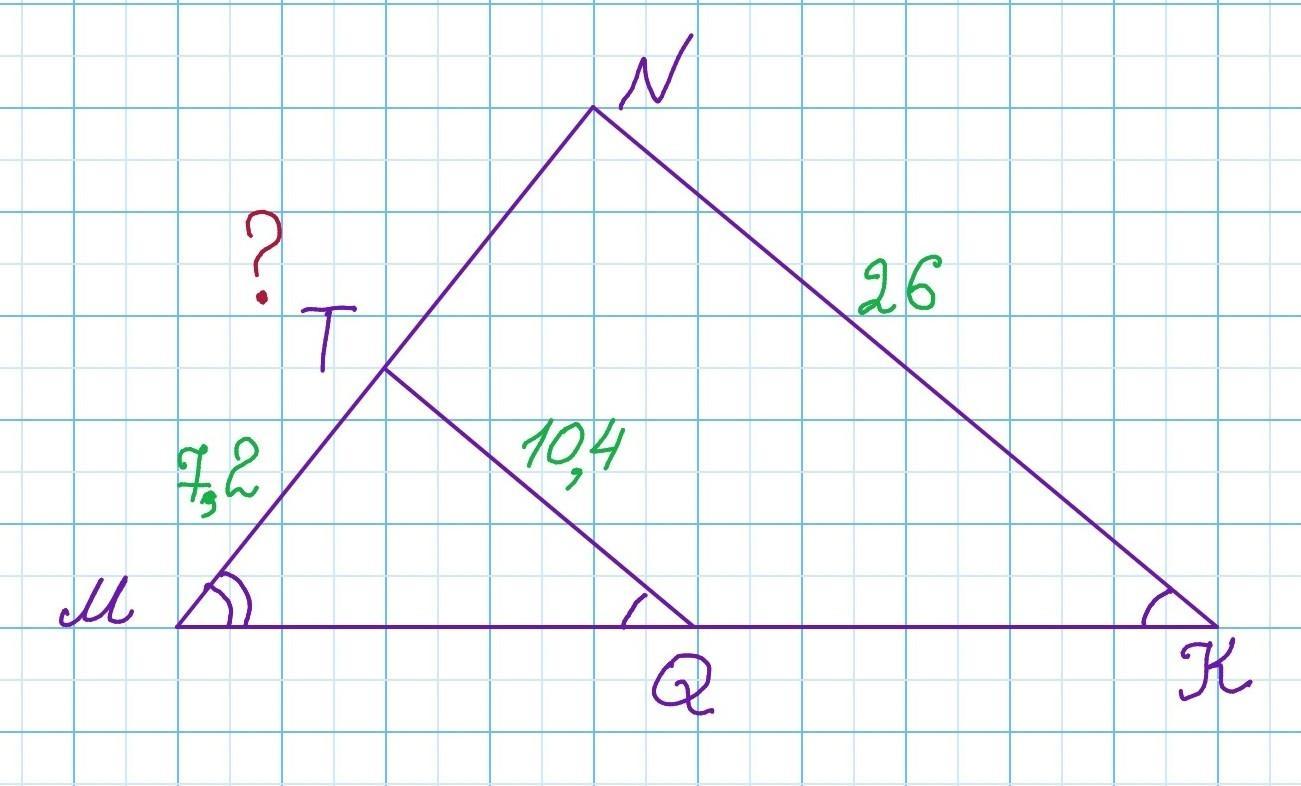
В треугольнике MNK провели прямую, параллельную стороне NK так, что она пересекает стороны MK и MN в точках Q и T соответственно. Найди длину стороны MN, если NK = 26, TQ = 10,4, MT = 7,2.
Ответы
Автор ответа:
11
Ответ:
MN = 18
Объяснение:
Треугольник NMK подобен треугольнику TMQ: угол М-общий, <NKM=<TQM- как внутренние накрест лежащие при параллельных прямых NK и TQ и секущей МК. (первый признак подобия)
Из подобия треугольников следует подобие сторон:
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Darigaaaaa
Предмет: Русский язык,
автор: elen301
Предмет: Русский язык,
автор: Аноним
Предмет: История,
автор: Saba456
Предмет: Литература,
автор: сложныеуроки2007