Предмет: Математика,
автор: grohdena
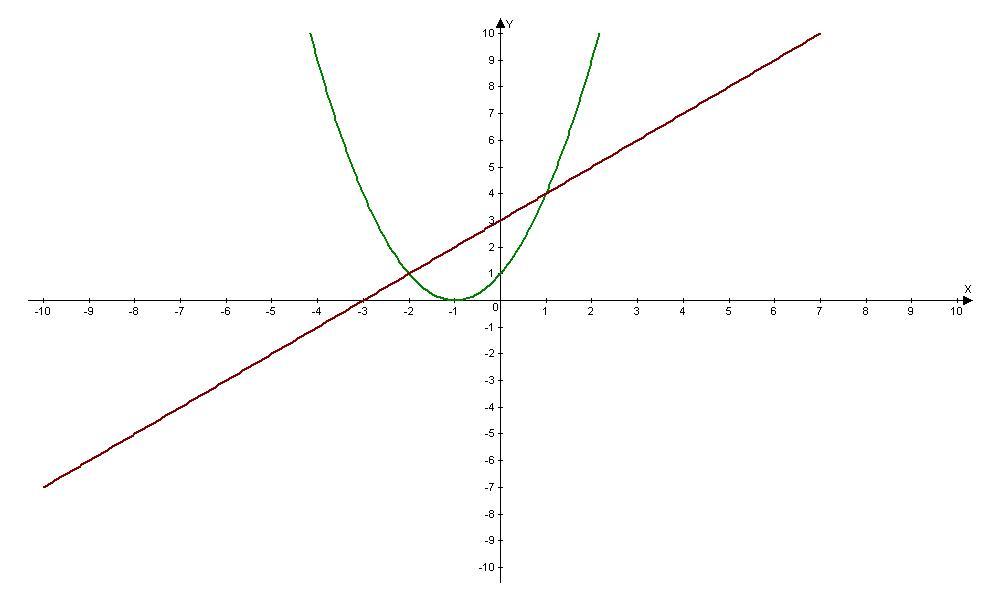
Знайти площу фігури обмеженої параболою y=x^2+2x+1 і прямою y=x+3
Помогите пж, даю 70 балов!!!
Ответы
Автор ответа:
1
Графиком функции y = x² + 2x + 1 = (x+1)² является парабола, ветви которой направлены вверх, её координаты вершины (-1;0).
y = x + 3 - прямая, проходящая через точки (-3;0), (0;3).
кв. ед.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: akasuhrob
Предмет: Другие предметы,
автор: Аноним
Предмет: Английский язык,
автор: АННААНГЕЛИНА1
Предмет: Математика,
автор: rezelenchuk1108
Предмет: Английский язык,
автор: Dima5604